Please solve this using python. Please show the code and explain!

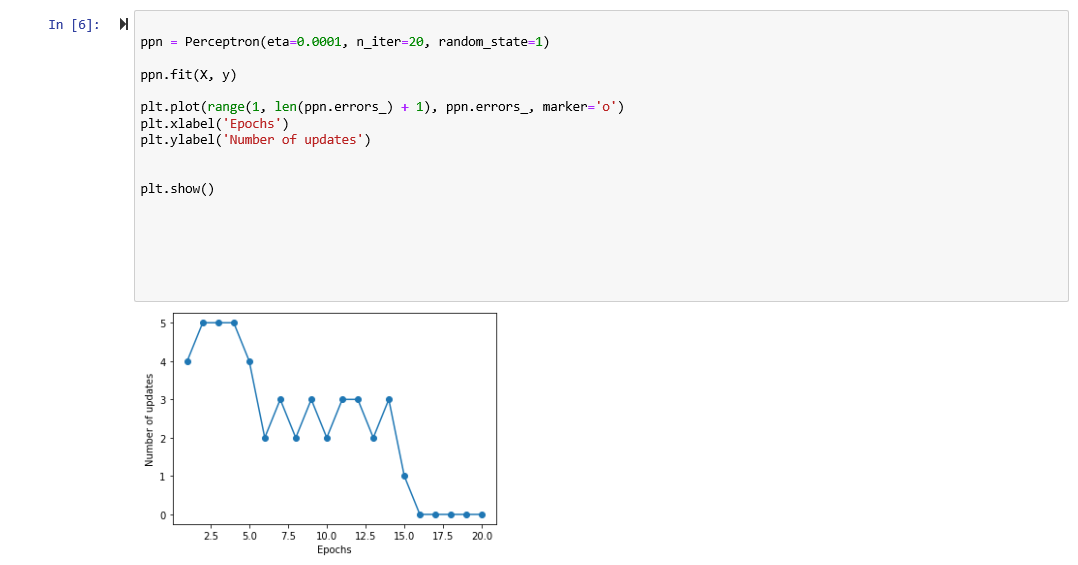
The following code is the perceptron implementation from the textbook (with only three lines inserted). In [5]: Nimport numpy as np class Perceptron(object): ** Perceptron classifier. Parameters eta : float Learning rate (between 0.2 and 1.0) n iter : int Passes over the training dataset. random_state : int Random number generator seed for random weight initialization. Attributes W 1d-array Weights after fitting. errors: list Number of misclassifications (updates) in each epoch. def __init__(self, eta=0.01, n_iter-50, random_state-1): self.eta - eta self.n_iter = niter self.random_state = random_state def fit(self, x, y): **Fit training data. Parameters X : {array-like), shape = [n_examples, n_features] Training vectors, where n_examples is the number of examples and n_features is the number of features. y : array-like, shape = [n_examples] Target values. Returns self : object rgen - np.random. RandomState(self.random_state) self.w = rgen.normal(loc-2.0, scale-0.01, size-1 + X.shape[1]) self.errors = [] for _ in range(self.n_iter): errors = 0 for xi, target in zip(x, y): update = self.eta * (target - self.predict(xi)) self.w_[1:] += update * xi self.w_[@] += update errors += int(update != 0.6) self.errors_.append(errors) # my do-nothing code IK = 2020 # my do-nothing code return self def net input(self, x): **"Calculate net input" return np.dot(X, self.w_[1:)) + self.w_[@] def predict(self, x): ***"Return class label after unit step""" return np.where(self.net_input(x) >= 0.0, 1, -1) In [6]: N ppn = Perceptron(eta=0.0001, n_iter=20, random_state=1) ppn.fit(x, y) plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors, marker='0') plt.xlabel('Epochs') plt.ylabel('Number of updates') plt.show() Number of updates 25 50 75 10.0 12.5 Epochs 15.0 17.5 20.0 Question 3: Visualizing multiple decision regions over time Here is the function for visualizing decision regions In [7]: from matplotlib.colors import ListedColormap def plot_decision_regions(x, y, classifier, resolution=0.02): # setup marker generator and color map markers = ('s', 'x', 'o', 'A', 'v') colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan') cmap = ListedColormap(colors[:len(np.unique(y)))) # plot the decision surface x1_min, x1_max = X[:, ].min() - 1, X[:, ].max() + 1 X2_min, X2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx1, xx2 = np.meshgrid(np.arange (x1_min, x1_max, resolution), np.arange (x2_min, X2_max, resolution)) Z = classifier.predict(np.array([xxl.ravel(), xx2.ravel()]).T) Z = Z.reshape(xxl.shape) plt.contourf(xxl, xx2, Z, alpha=0.3, cmap=cmap) plt.xlim(xx1.min(), xx1.max()) plt.ylim(xx2.min(), Xx2.max()) # plot class examples for idx, cl in enumerate(np.unique(y)): plt. scatter(x=X[y == cl, ], y=X[y == cl, 1], alpha=0.8, C=colors[idx] marker=markers[idx), label=cl, edgecolor='black') In [8]: plot_decision_regions(x, y, classifier=ppn) plt.xlabel('sepal length [cm]') plt.ylabel('petal length [cm]') plt. legend(loc='upper left') # plt. savefig('images/02_08.png', dpi=300) plt.show() petal length (cm) sepal length (cm) Using the above, give code that plots the decision regions for the first 5 epochs. Use learning rate = 0.01 and random seed = 1 when applicable. In [9]: # The following code is the perceptron implementation from the textbook (with only three lines inserted). In [5]: Nimport numpy as np class Perceptron(object): ** Perceptron classifier. Parameters eta : float Learning rate (between 0.2 and 1.0) n iter : int Passes over the training dataset. random_state : int Random number generator seed for random weight initialization. Attributes W 1d-array Weights after fitting. errors: list Number of misclassifications (updates) in each epoch. def __init__(self, eta=0.01, n_iter-50, random_state-1): self.eta - eta self.n_iter = niter self.random_state = random_state def fit(self, x, y): **Fit training data. Parameters X : {array-like), shape = [n_examples, n_features] Training vectors, where n_examples is the number of examples and n_features is the number of features. y : array-like, shape = [n_examples] Target values. Returns self : object rgen - np.random. RandomState(self.random_state) self.w = rgen.normal(loc-2.0, scale-0.01, size-1 + X.shape[1]) self.errors = [] for _ in range(self.n_iter): errors = 0 for xi, target in zip(x, y): update = self.eta * (target - self.predict(xi)) self.w_[1:] += update * xi self.w_[@] += update errors += int(update != 0.6) self.errors_.append(errors) # my do-nothing code IK = 2020 # my do-nothing code return self def net input(self, x): **"Calculate net input" return np.dot(X, self.w_[1:)) + self.w_[@] def predict(self, x): ***"Return class label after unit step""" return np.where(self.net_input(x) >= 0.0, 1, -1) In [6]: N ppn = Perceptron(eta=0.0001, n_iter=20, random_state=1) ppn.fit(x, y) plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors, marker='0') plt.xlabel('Epochs') plt.ylabel('Number of updates') plt.show() Number of updates 25 50 75 10.0 12.5 Epochs 15.0 17.5 20.0 Question 3: Visualizing multiple decision regions over time Here is the function for visualizing decision regions In [7]: from matplotlib.colors import ListedColormap def plot_decision_regions(x, y, classifier, resolution=0.02): # setup marker generator and color map markers = ('s', 'x', 'o', 'A', 'v') colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan') cmap = ListedColormap(colors[:len(np.unique(y)))) # plot the decision surface x1_min, x1_max = X[:, ].min() - 1, X[:, ].max() + 1 X2_min, X2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx1, xx2 = np.meshgrid(np.arange (x1_min, x1_max, resolution), np.arange (x2_min, X2_max, resolution)) Z = classifier.predict(np.array([xxl.ravel(), xx2.ravel()]).T) Z = Z.reshape(xxl.shape) plt.contourf(xxl, xx2, Z, alpha=0.3, cmap=cmap) plt.xlim(xx1.min(), xx1.max()) plt.ylim(xx2.min(), Xx2.max()) # plot class examples for idx, cl in enumerate(np.unique(y)): plt. scatter(x=X[y == cl, ], y=X[y == cl, 1], alpha=0.8, C=colors[idx] marker=markers[idx), label=cl, edgecolor='black') In [8]: plot_decision_regions(x, y, classifier=ppn) plt.xlabel('sepal length [cm]') plt.ylabel('petal length [cm]') plt. legend(loc='upper left') # plt. savefig('images/02_08.png', dpi=300) plt.show() petal length (cm) sepal length (cm) Using the above, give code that plots the decision regions for the first 5 epochs. Use learning rate = 0.01 and random seed = 1 when applicable. In [9]: #