Please solve using Matlab and Conditional Statements(such as if, elseif, else). To receive a thumbs up DO NOT USE ITERATIONS(aka Loops) in the solution code!!!

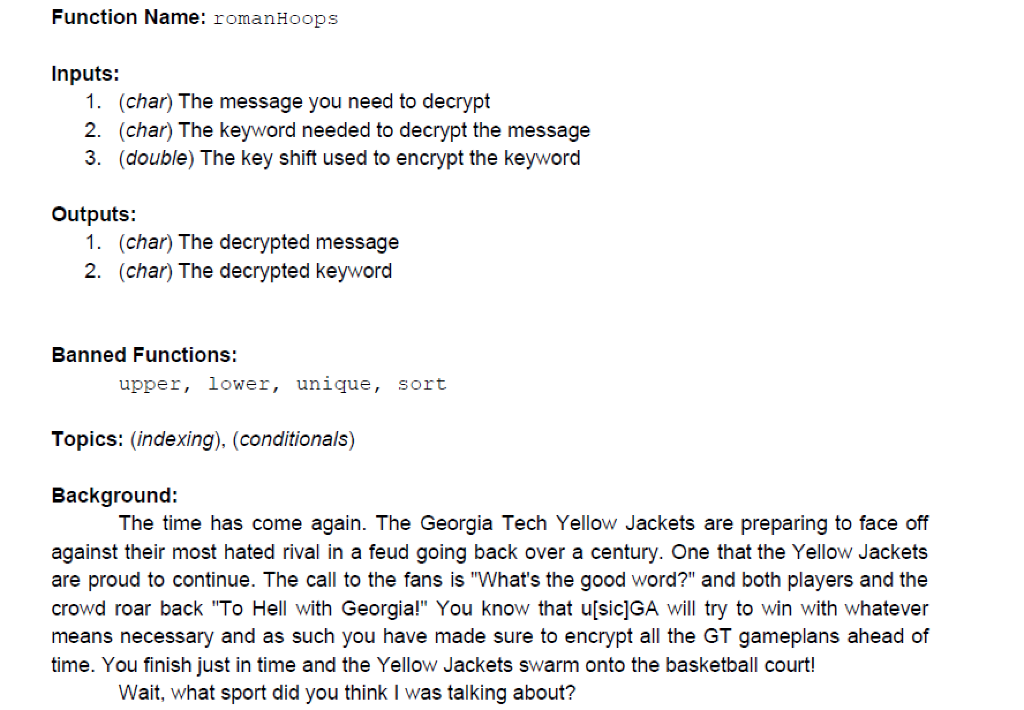
Function Name: romanHoops Inputs: 1. (char) The message you need to decrypt 2. (char) The keyword needed to decrypt the message 3. (double) The key shift used to encrypt the keyword Outputs: 1. (char) The decrypted message 2. (char) The decrypted keyword Banned Functions: upper, lower, unique, sort Topics: indexing), (conditionals) Background: The time has come again. The Georgia Tech Yellow Jackets are preparing to face off against their most hated rival in a feud going back over a century. One that the Yellow Jackets are proud to continue. The call to the fans is "What's the good word?" and both players and the crowd roar back "To Hell with Georgia!" You know that u[sic]GA will try to win with whatever means necessary and as such you have made sure to encrypt all the GT gameplans ahead of time. You finish just in time and the Yellow Jackets swarm onto the basketball court! Wait, what sport did you think I was talking about? Function Description: The eponymous caesar cipher is one of the most widely known encryption techniques. To use it you simply shift the alphabet left by a certain number of characters, wrapping back around to the end, and then replace all the letters with their new equivalents. A shift of 1 would see A become B, B become c, and so on until Z becomes A. A shift of 2 would have A become C, B become D, and so on until Z becomes B. Unfortunately, this cipher is easily decrypted as there are only 25 possible ways to encrypt a message with it. (Replacing A with A does not actually encrypt a message.) As such there have been multiple variations of the caesar cipher developed, many of which use a keyword in addition to a shift number, including the one you will implement in MATLAB. Write a function that decrypts an encrypted message input 1). Given the encrypted keyword (input 2), perform the following steps to obtain the decrypted keyword. 1. Make all letters lowercase and remove all punctuation, numbers, and spaces. 2. Remove repeated letters. 3. Perform a simple caesar cipher with the given shift number (input 3). Next, declare two new variables which we will call shiftA and shifts. Assign the positive distance between the first and last characters to shifta. Assign the positive distance between the second and second-to-last characters to shifts. For example, if your decrypted keyword is: decKeyword hellothere then: shifta shifts If shiftA ends up equaling zero, use the value 1 for shiftA. Likewise, if shifti ends up equalling zero, use the value 2 for shiftB. Depending on the most common letter in the decrypted keyword, each shift number will be applied to different parts of the original message in another simple caesar cipher. If the most common letter in the resulting decrypted keyword is... ... a consonant and an odd alphabetical character (c is #3 in the alphabet, so it is odd) use shifta on the odd indices of the encrypted message and shifts on the even indices. ... a consonant and an even alphabetical character (b is #2 in the alphabet, so it is even), apply shiftA to every odd character in the encrypted message and shifts on the even ones. In this case, if one shift number is even and the other odd, double the odd one. a vowel (not including y), the first half of the encrypted message will be decrypted with shifta, and the second half of the encrypted message will be decrypted with shiftB. Should the message be of odd length, the halfway point is determined by whichever character next to the middle one is larger, with the corresponding side containing the middle character. For example, if the message is: msg 'gibberish' Compare the b to the r. Since r is "greater" than b, the e goes to the second half: first Half secondHalf 'gibb 'erish' Do not forget to recombine the two halves of the message. The resulting string, once these operations are performed, is your decrypted message. Output this along with the decrypted keyword. Example: encMsg = 'Tfobuvt Qpqvmaywak Xusgtay' key = 'U!rr pp.352453xxox.xvv' shift = 3 [decMsg, key] = romanHoops (encMsg, key, shift) key 'romulus' decMsg 'Senatus Populusque Romanus' . Notes: Do not change any of the capitalization of punctuation when performing a caesar cipher A and C are odd alphabetical characters, while B is even. B is larger than A while smaller than C. These pattern/trend hold throughout the alphabet The shift number will never be negative Every keyword will have at least 4 unique letters There will never be a tie between which letters in the keyword are the most common Letters in the keyword will never repeat more than once . Function Name: romanHoops Inputs: 1. (char) The message you need to decrypt 2. (char) The keyword needed to decrypt the message 3. (double) The key shift used to encrypt the keyword Outputs: 1. (char) The decrypted message 2. (char) The decrypted keyword Banned Functions: upper, lower, unique, sort Topics: indexing), (conditionals) Background: The time has come again. The Georgia Tech Yellow Jackets are preparing to face off against their most hated rival in a feud going back over a century. One that the Yellow Jackets are proud to continue. The call to the fans is "What's the good word?" and both players and the crowd roar back "To Hell with Georgia!" You know that u[sic]GA will try to win with whatever means necessary and as such you have made sure to encrypt all the GT gameplans ahead of time. You finish just in time and the Yellow Jackets swarm onto the basketball court! Wait, what sport did you think I was talking about? Function Description: The eponymous caesar cipher is one of the most widely known encryption techniques. To use it you simply shift the alphabet left by a certain number of characters, wrapping back around to the end, and then replace all the letters with their new equivalents. A shift of 1 would see A become B, B become c, and so on until Z becomes A. A shift of 2 would have A become C, B become D, and so on until Z becomes B. Unfortunately, this cipher is easily decrypted as there are only 25 possible ways to encrypt a message with it. (Replacing A with A does not actually encrypt a message.) As such there have been multiple variations of the caesar cipher developed, many of which use a keyword in addition to a shift number, including the one you will implement in MATLAB. Write a function that decrypts an encrypted message input 1). Given the encrypted keyword (input 2), perform the following steps to obtain the decrypted keyword. 1. Make all letters lowercase and remove all punctuation, numbers, and spaces. 2. Remove repeated letters. 3. Perform a simple caesar cipher with the given shift number (input 3). Next, declare two new variables which we will call shiftA and shifts. Assign the positive distance between the first and last characters to shifta. Assign the positive distance between the second and second-to-last characters to shifts. For example, if your decrypted keyword is: decKeyword hellothere then: shifta shifts If shiftA ends up equaling zero, use the value 1 for shiftA. Likewise, if shifti ends up equalling zero, use the value 2 for shiftB. Depending on the most common letter in the decrypted keyword, each shift number will be applied to different parts of the original message in another simple caesar cipher. If the most common letter in the resulting decrypted keyword is... ... a consonant and an odd alphabetical character (c is #3 in the alphabet, so it is odd) use shifta on the odd indices of the encrypted message and shifts on the even indices. ... a consonant and an even alphabetical character (b is #2 in the alphabet, so it is even), apply shiftA to every odd character in the encrypted message and shifts on the even ones. In this case, if one shift number is even and the other odd, double the odd one. a vowel (not including y), the first half of the encrypted message will be decrypted with shifta, and the second half of the encrypted message will be decrypted with shiftB. Should the message be of odd length, the halfway point is determined by whichever character next to the middle one is larger, with the corresponding side containing the middle character. For example, if the message is: msg 'gibberish' Compare the b to the r. Since r is "greater" than b, the e goes to the second half: first Half secondHalf 'gibb 'erish' Do not forget to recombine the two halves of the message. The resulting string, once these operations are performed, is your decrypted message. Output this along with the decrypted keyword. Example: encMsg = 'Tfobuvt Qpqvmaywak Xusgtay' key = 'U!rr pp.352453xxox.xvv' shift = 3 [decMsg, key] = romanHoops (encMsg, key, shift) key 'romulus' decMsg 'Senatus Populusque Romanus' . Notes: Do not change any of the capitalization of punctuation when performing a caesar cipher A and C are odd alphabetical characters, while B is even. B is larger than A while smaller than C. These pattern/trend hold throughout the alphabet The shift number will never be negative Every keyword will have at least 4 unique letters There will never be a tie between which letters in the keyword are the most common Letters in the keyword will never repeat more than once