Please solve using the Excel Solver, if possible.

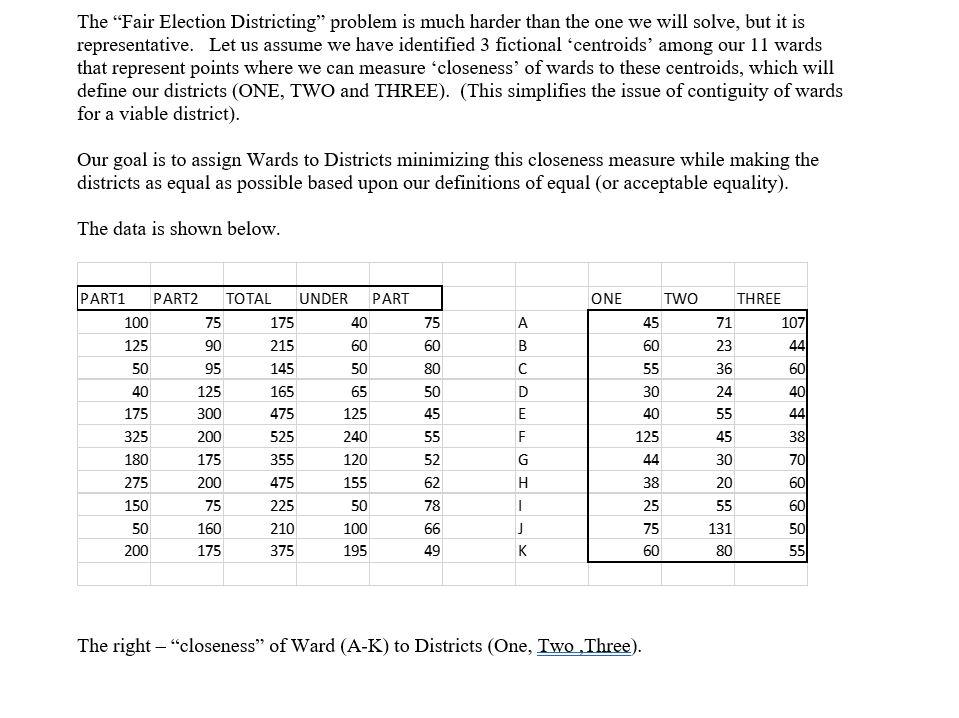
The "Fair Election Districting" problem is much harder than the one we will solve, but it is representative. Let us assume we have identified 3 fictional centroids' among our 11 wards that represent points where we can measure 'closeness' of wards to these centroids, which will define our districts (ONE, TWO and THREE). (This simplifies the issue of contiguity of wards for a viable district). Our goal is to assign Wards to Districts minimizing this closeness measure while making the districts as equal as possible based upon our definitions of equal (or acceptable equality). The data is shown below. ONE 75 75 A B C PART1 PART2 TOTAL UNDER PART 100 175 40 125 90 215 60 50 95 145 50 40 125 165 65 175 300 475 125 325 200 525 240 180 175 355 120 275 200 475 155 150 75 225 50 50 160 210 100 200 175 375 195 D E F 60 80 50 45 55 52 62 78 66 49 TWO 45 60 55 30 40 125 44 38 25 75 60 THREE 71 1071 23 44 36 24 40 55 44 45 38 30 70 20 60 55 131 50 80 55 G H 1 J K The right - "closeness" of Ward (A-K) to Districts (One, Two, Three). PARTI.PART2 the number of registered voters of party (1,2). TOTAL the total number of registered votes in that ward (we are ignoring independents). UNDER - the number of registered voters that are members of underrepresented groups. PART - a measure of how that ward participated in elections (Higher is better). (You can assume the units are thousands, though that doesn't matter). Create a plan on which wards are assigned to which congressional districts such that closeness is minimized and the following guidelines are met. 1) Each district should have between 1050 and 1200 voters, inclusive of the end points. 2) Each party cannot make up less that 45% of the total voters in that district. 3) Participation (at the ward level) must average at least 60 units for each district. Note that this is NOT population weighted - all wards 'count equally. 4) Each district must have at 30% of its voters be of the underrepresented group. 5) Wards cannot be assigned to districts if their closeness is greater than 100. Summarize your solution and show how close to 'equal' these parameters direct the solver to 'equality. Note that the Solver might struggle with solving this model - please uncheck the use Automatic Scaling box in options as a safe guard. As always, I reserve the right to change the problem requirements should an error be identified. And ... I would be curious if any of you can come up with a more equal' solution in any way. If we had more time, I'd love to play around with the Open Solver a better binary solution algorithm) with this problem. Version 1- last update 11/16 The "Fair Election Districting" problem is much harder than the one we will solve, but it is representative. Let us assume we have identified 3 fictional centroids' among our 11 wards that represent points where we can measure 'closeness' of wards to these centroids, which will define our districts (ONE, TWO and THREE). (This simplifies the issue of contiguity of wards for a viable district). Our goal is to assign Wards to Districts minimizing this closeness measure while making the districts as equal as possible based upon our definitions of equal (or acceptable equality). The data is shown below. ONE 75 75 A B C PART1 PART2 TOTAL UNDER PART 100 175 40 125 90 215 60 50 95 145 50 40 125 165 65 175 300 475 125 325 200 525 240 180 175 355 120 275 200 475 155 150 75 225 50 50 160 210 100 200 175 375 195 D E F 60 80 50 45 55 52 62 78 66 49 TWO 45 60 55 30 40 125 44 38 25 75 60 THREE 71 1071 23 44 36 24 40 55 44 45 38 30 70 20 60 55 131 50 80 55 G H 1 J K The right - "closeness" of Ward (A-K) to Districts (One, Two, Three). PARTI.PART2 the number of registered voters of party (1,2). TOTAL the total number of registered votes in that ward (we are ignoring independents). UNDER - the number of registered voters that are members of underrepresented groups. PART - a measure of how that ward participated in elections (Higher is better). (You can assume the units are thousands, though that doesn't matter). Create a plan on which wards are assigned to which congressional districts such that closeness is minimized and the following guidelines are met. 1) Each district should have between 1050 and 1200 voters, inclusive of the end points. 2) Each party cannot make up less that 45% of the total voters in that district. 3) Participation (at the ward level) must average at least 60 units for each district. Note that this is NOT population weighted - all wards 'count equally. 4) Each district must have at 30% of its voters be of the underrepresented group. 5) Wards cannot be assigned to districts if their closeness is greater than 100. Summarize your solution and show how close to 'equal' these parameters direct the solver to 'equality. Note that the Solver might struggle with solving this model - please uncheck the use Automatic Scaling box in options as a safe guard. As always, I reserve the right to change the problem requirements should an error be identified. And ... I would be curious if any of you can come up with a more equal' solution in any way. If we had more time, I'd love to play around with the Open Solver a better binary solution algorithm) with this problem. Version 1- last update 11/16