Please teach how to solve question c, only question c Thank you

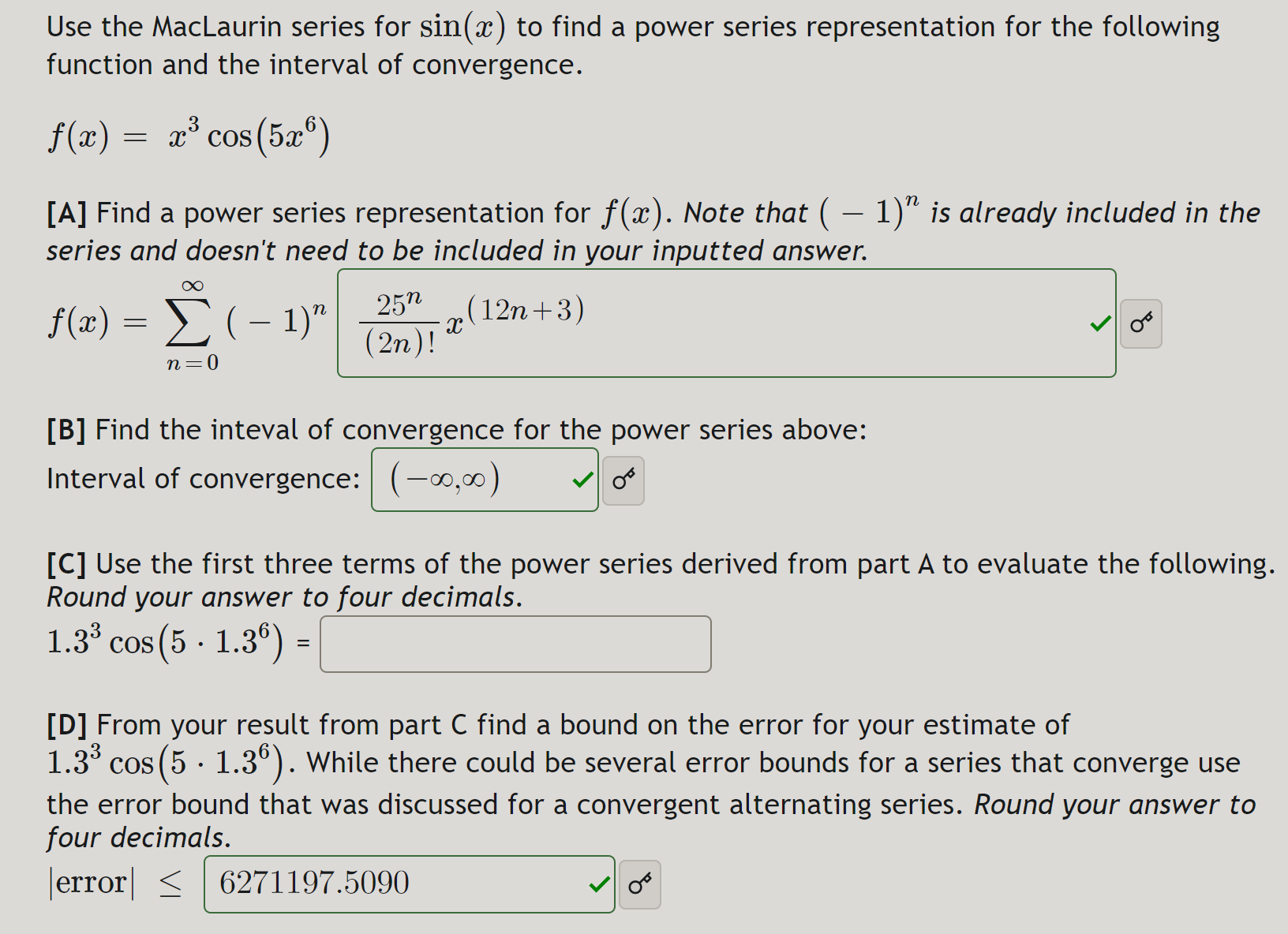
Use the MacLaurin series for sin(x ) to find a power series representation for the following function and the interval of convergence. f(ac) = 23 cos (526) [A] Find a power series representation for f(x). Note that ( - 1)" is already included in the series and doesn't need to be included in your inputted answer. f ( 2 ) = E ( - 1 ) " 25n (12n +3) (2n) ! n= 0 [B] Find the inteval of convergence for the power series above: Interval of convergence: (-00,00) [C] Use the first three terms of the power series derived from part A to evaluate the following. Round your answer to four decimals. 1.3 cos (5 . 1.36) = [D] From your result from part C find a bound on the error for your estimate of 1.39 cos (5 . 1.3). While there could be several error bounds for a series that converge use the error bound that was discussed for a convergent alternating series. Round your answer to four decimals. error