Please tell me how I can do this in Excel, and what is the final correct solution? I tried to find the average profit, but I couldn't. I sent you the question below. Check it out too take pictures

First, simulate using the order size as the decision variable as follows: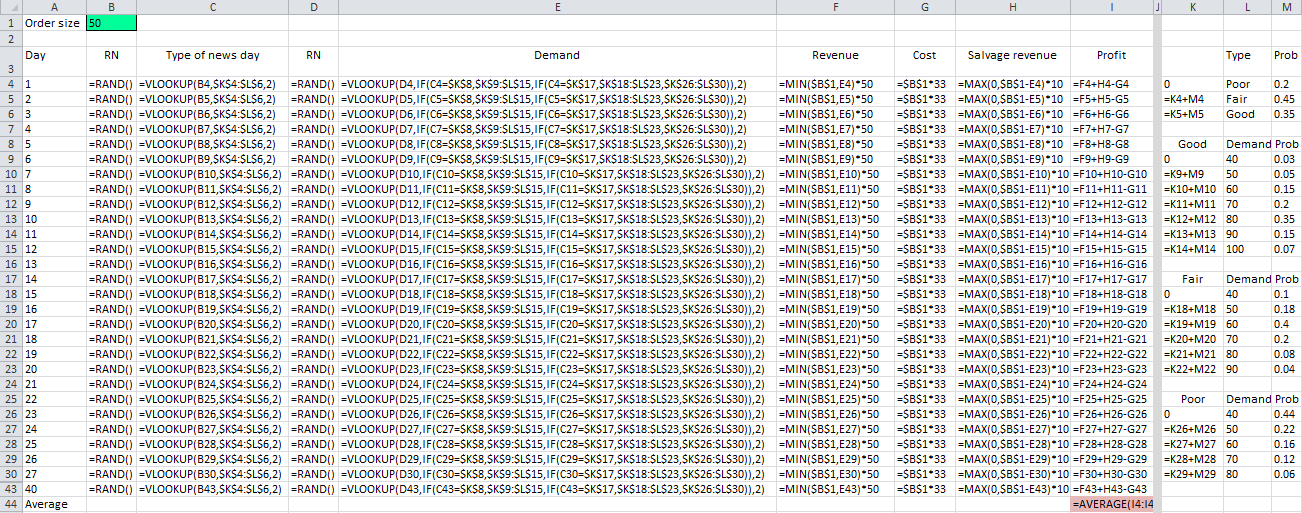

Now, use the data table option (Data --> What-if analysis --> Data table) to populate the average profit by varying the order size as follows:

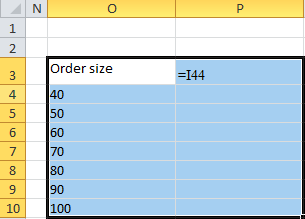
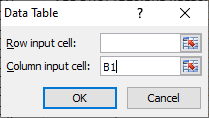
Result:

Order size	Average Profit
40	680
50	810
60	930
70	770
80	720
90	540
100	240

As we can see, the average profit per day is maximized with an order size of 60 units.

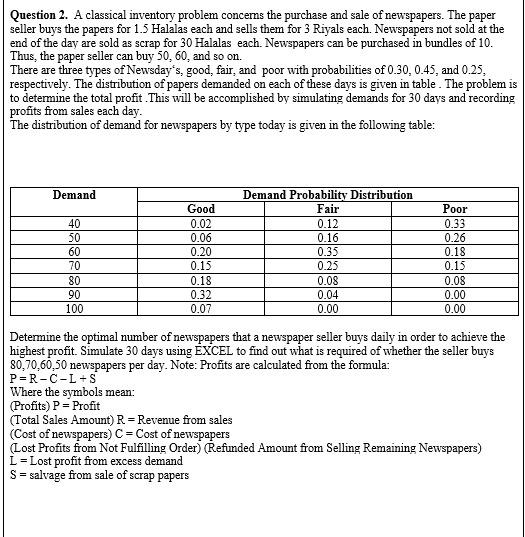
Good A B D E F G H 1 K L M 1 Order size 50 1 2 Day RN Type of news day RN Demand Revenue Cost Salvage revenue Profit Type Prob 3 4 1 =RAND() =VLOOKUP(B4,$K$4:$L$6,2)=RAND() =VLOOKUP(D4, IF(C4=$K$8,$K$9:$L$15,IF(C4=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E4)*50 =$B$1*33 =MAX(0,$B$1-E4)*10 =F4+H4-G4 0 Poor 0.2 5 5 2 =RAND() =VLOOKUP(B5,$K$4:$L$6,2)=RAND() =VLOOKUP(D5, 1F (C5=$K$8,$K$9:$L$15,IF(C5=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =K, K$$$ =MIN($B$1,E5)*50 =$B$1*33 =MAX(0,$B$1-E5)*10 =F5+H5-G5 =K4+M4 Fair 0.45 63 6 =RAND() =VLOOKUP(B6,$K$4:$L$6,2)=RAND() =VLOOKUP(D6,1F(C6=$K$8,$K$9:$L$15, IF(C6=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E6)*50 =$B$1.33 =MAX(0,$B$1-E6)*10 =F6+H6-66 =K5+M5 Good 0.35 74 =RANDO) =VLOOKUP(B7,$K$4:$L$6,2)=RAND() =VLOOKUP(D7,IF(C7=$K$8,$K$9:$L$15,IF(C7=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E7)*50 =$B$1.33 =MAX(0,$B$1-E7) 10 =F7+H7-G7 8 5 =RAND() =VLOOKUP(B8,$K$4:$L$6,2)=RAND() =VLOOKUP(D8,IF(C8=$K$8,$K$9:$L$15,1F (C8=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E8)*50 =$B$1*33 =MAX(0,$B$1-E8)*10 =F8+H8-G8 Demand Prob 96 =RAND() =VLOOKUP(B9,$K$4:$L$6,2)=RAND() =VLOOKUP(D9,IF(C9=$K$8,$K$9:$L$15,IF(C9=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E9)*50 =$B$1.33 =MAX(0,$B$1-E9)10 =F9+H9-G9 0 40 0.03 10 7 =RANDO) =VLOOKUP(B10,$K$4:$L$6,2) =RAND() =VLOOKUP(D10,IF(C10=$K$8,$K$9:$L$15,IF(C10=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E10)*50 =$B$1.33 =MAX(0,$B$1-E10) * 10 =F10+H10-G10 =K9+M9 50 0.05 11 8 =RANDO) =VLOOKUP(B11,$K$4:$L$6,2) =RAND() =VLOOKUP(D11,IF(C11=$K$8,$K$9:$L$15,IF(C11=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E11)*50 =$B$1.33 =MAX(0,$B$1-E11)*10 =F11+H11-G11 =K10+M10 60 0.15 129 =RAND() =VLOOKUP(B12,$K$4:$L$6,2) =RAND() =VLOOKUP(D12,IF(C12=$K$8,$K$9:$L$15,IF(C12=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E12)*50 =$B$1*33 =MAX(0,$B$1-E12) 10 =F12+H12-G12 =K11+M11 70 0.2 13 10 =RAND() =VLOOKUP(B13,$K$4:$L$6,2) =RAND() =VLOOKUP(D13,IF(C13=$K$8,$K$9:$L$15,IF(C13=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E13)*50 =$B$1*33 =MAX(0,$B$1-E13)*10 =F13+H13-G13 =K12+M12 80 0.35 14 11 =RANDO) =VLOOKUP(B14,$K$4:$L$6,2) =RAND() =VLOOKUP(D14,IF(C14=$K$8,$K$9:$L$15,1F(C14=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E14)*50 -$B$1.33 =MAX(0,$B$1-E14) 10 =F14+H14-G14 =K13+M13 90 0.15 15 12 =RAND() =VLOOKUP(B15,$K$4:$L$6,2) =RAND() =VLOOKUP(D15, IF(C15-$K$8,$K$9:$L$15,IF(C15-$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E15)*50 =$B$1*33 =MAX(0,$B$1-E15)*10 =F15+H15-G15 =K14+M14 100 0.07 16 13 =RAND() =VLOOKUP(B16,$K$4:$L$6,2) =RAND() =VLOOKUP(D16,IF(C16=$K$8,$K$9:$L$15,1F(C16=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E16)*50 =$B$1.33 =MAX(0,$B$1-E16)*10 =F16+H16-G16 17 14 =RAND() =VLOOKUP(B17,$K$4:$L$6,2) =RAND() =VLOOKUP(D17,1F(C17=$K$8,$K$9:$L$15,1F(C17=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E17)*50 =$B$1*33 =MAX(0,$B$1-E17)*10 =F17+H17-G17 Fair Demand Prob 18 15 =RAND() =VLOOKUP(B18,$K$4:$L$6,2) =RAND() =VLOOKUP(D18,IF(C18=$K$8,$K$9:$L$15,IF(C18=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E18)*50 =$B$1.33 =MAX(0,$B$1-E18)*10 =F18+H18-G18 0 40 0.1 19 16 =RAND() =VLOOKUP(B19,$K$4:$L$6,2) =RAND() =VLOOKUP(D19,IF(C19-$K$8,$K$9:$L$15,IF(C19=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E19)*50 =$B$1*33 =MAX(0,$B$1-E19)*10 =F19+H19-G19 =K18+M18 50 0.18 20 17 =RAND() =VLOOKUP(B20,$K$4:$L$6,2) =RAND() =VLOOKUP(D20,1F(C20=$K$8,$K$9:$L$15,1F(C20-$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E20)*50 =$B$1*33 =MAX(0,$B$1-E20)*10 =F20+H20-G20 =K19+M19 60 0.4 21 18 =RAND() =VLOOKUP(B21,$K$4:$L$6,2) =RAND() =VLOOKUP(D21,IF(C21=$K$8,$K$9:$L$15,IF(C21=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E21)*50 =$$L$=$$$KK$$$))2 =$B$1*33 =MAX(0,$B$1-E21) 10 =F21+H21-G21 =K20+M20 70 0.2 22 19 =RAND() =VLOOKUP(B22,$K$4:$L$6,2) =RAND() =VLOOKUP(D22,IF(C22=$K$8,$K$9:$L$15,IF(C22=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E22)*50 =$B$1*33 =MAX(0,$B$1-E22)* 10 =F22+H22-G22 =K21+M21 80 0.08 23 20 =RAND() =VLOOKUP(B23,$K$4:$L$6,2) =RAND() =VLOOKUP(D23,IF(C23=$K$8,$K$9:$L$15,IF(C23=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E23)*50 =$B$1*33 =MAX(0,$B$1-E23)*10 =F23+H23-G23 =K22+M22 90 0.04 24 21 =RAND() =VLOOKUP(B24,$K$4:$L$6,2) =RAND() =VLOOKUP(D24, IF(C24=$K$8,$K$9:$L$15,IF(C24=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E24)*50 =$B$1*33 =MAX(0,$B$1-E24)*10 =F24+H24-G24 25 22 =RANDO) =VLOOKUP(B25,$K$4:$L$6,2) =RAND() =VLOOKUP(D25,IF(C25=$K$8,$K$9:$L$15,IF(C25=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E25)*50 =$B$1.33 =MAX(0,$B$1-E25)* 10 =F25+H25-G25 Poor Demand Prob 26 23 =RAND() =VLOOKUP(B26,$K$4:$L$6,2) =RAND() =VLOOKUP(D26,IF(C26=$K$8,$K$9:$L$15,1F(C26=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E26)*50=$B$1*33 =MAX(0,$B$1-E26)*10 =F26+H26-G26 $( 0 40 0.44 27 24 =RAND() =VLOOKUP(B27,$K$4:$L$6,2) =RAND() =VLOOKUP(D27,IF(C27=$K$8,$K$9:$L$15,1F(C27=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E27)*50 =$B$1.33 =MAX(0,$B$1-E27)*10 =F27+H27-G27 =K26+M26 50 0.22 28 25 =RAND() =VLOOKUP(B28,$K$4:$L$6,2) =RAND() =VLOOKUP(D28,IF(C28=$K$8,$K$9:$L$15,IF(C28=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E28)*50 =$B$1*33 =MAX(0,$B$1-E28)* 10 =F28+H28-628 =K27+M27 60 0.16 29 26 =RANDO) =VLOOKUP(B29,$K$4:$L$6,2) =RAND() =VLOOKUP(D29,IF(C29=$K$8,$K$9:$L$15,IF(C29=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E29)*50 =$B$1.33 =MAX(0,$B$1-E29)*10 =F29+H29-G29 =K28+M28 70 0.12 30 27 =RAND() =VLOOKUP(B30,$K$4:$L$6,2) =RAND() =VLOOKUP(D30,1F(C30=$K$8,$K$9:$L$15,IF(C30-$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E30)*50 =$B$1.33 =MAX(0,$B$1-E30) 10 =F30+H30-G30 $=K$=K$$$B, =K29+M29 80 0.06 43 40 =RANDO) =VLOOKUP(B43,$K$4:$L$6,2) =RAND() =VLOOKUP(D43,IF(C43=$K$8,$K$9:$L$15,IF(C43=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E43)*50 =$B$1*33 =MAX(0,$B$1-E43)*10 =F43+H43-643 44 Average =AVERAGE(14:14 N o P 1 2 Order size =144 3 4 5 0 00 N O uw 40 50 60 6 7 8 9 10 70 80 90 100 Data Table ? X x Row input cell: Column input cell: B11 OK Cancel Question 2. A classical inventory problem concerns the purchase and sale of newspapers. The paper seller buys the papers for 1.5 Halalas each and sells them for 3 Riyals each. Newspapers not sold at the end of the day are sold as scrap for 30 Halalas each. Newspapers can be purchased in bundles of 10. Thus, the paper seller can buy 50, 60, and so on. There are three types of Newsday's, good, fair, and poor with probabilities of 0.30, 0.45, and 0.25, respectively. The distribution of papers demanded on each of these days is given in table. The problem is to determine the total profit. This will be accomplished by simulating demands for 30 days and recording profits from sales each day. The distribution of demand for newspapers by type today is given in the following table: Demand 40 50 60 70 80 90 100 Good 0.02 0.06 0.20 0.15 0.18 0.32 0.07 Demand Probability Distribution Fair 0.12 0.16 0.35 0.25 0.08 0.04 0.00 Poor 0.33 0.26 0.18 0.15 0.08 0.00 0.00 Determine the optimal number of newspapers that a newspaper seller buys daily in order to achieve the highest profit. Simulate 30 days using EXCEL to find out what is required of whether the seller buys 80,70,60,50 newspapers per day. Note: Profits are calculated from the formula: P=R-C-L-S Where the symbols mean: (Profits) P = Profit (Total Sales Amount) R = Revenue from sales (Cost of newspapers) C = Cost of newspapers (Lost Profits from Not Fulfilling Order) (Refunded Amount from Selling Remaining Newspapers) L = Lost profit from excess demand S = salvage from sale of scrap papers Good A B D E F G H 1 K L M 1 Order size 50 1 2 Day RN Type of news day RN Demand Revenue Cost Salvage revenue Profit Type Prob 3 4 1 =RAND() =VLOOKUP(B4,$K$4:$L$6,2)=RAND() =VLOOKUP(D4, IF(C4=$K$8,$K$9:$L$15,IF(C4=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E4)*50 =$B$1*33 =MAX(0,$B$1-E4)*10 =F4+H4-G4 0 Poor 0.2 5 5 2 =RAND() =VLOOKUP(B5,$K$4:$L$6,2)=RAND() =VLOOKUP(D5, 1F (C5=$K$8,$K$9:$L$15,IF(C5=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =K, K$$$ =MIN($B$1,E5)*50 =$B$1*33 =MAX(0,$B$1-E5)*10 =F5+H5-G5 =K4+M4 Fair 0.45 63 6 =RAND() =VLOOKUP(B6,$K$4:$L$6,2)=RAND() =VLOOKUP(D6,1F(C6=$K$8,$K$9:$L$15, IF(C6=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E6)*50 =$B$1.33 =MAX(0,$B$1-E6)*10 =F6+H6-66 =K5+M5 Good 0.35 74 =RANDO) =VLOOKUP(B7,$K$4:$L$6,2)=RAND() =VLOOKUP(D7,IF(C7=$K$8,$K$9:$L$15,IF(C7=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E7)*50 =$B$1.33 =MAX(0,$B$1-E7) 10 =F7+H7-G7 8 5 =RAND() =VLOOKUP(B8,$K$4:$L$6,2)=RAND() =VLOOKUP(D8,IF(C8=$K$8,$K$9:$L$15,1F (C8=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E8)*50 =$B$1*33 =MAX(0,$B$1-E8)*10 =F8+H8-G8 Demand Prob 96 =RAND() =VLOOKUP(B9,$K$4:$L$6,2)=RAND() =VLOOKUP(D9,IF(C9=$K$8,$K$9:$L$15,IF(C9=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E9)*50 =$B$1.33 =MAX(0,$B$1-E9)10 =F9+H9-G9 0 40 0.03 10 7 =RANDO) =VLOOKUP(B10,$K$4:$L$6,2) =RAND() =VLOOKUP(D10,IF(C10=$K$8,$K$9:$L$15,IF(C10=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E10)*50 =$B$1.33 =MAX(0,$B$1-E10) * 10 =F10+H10-G10 =K9+M9 50 0.05 11 8 =RANDO) =VLOOKUP(B11,$K$4:$L$6,2) =RAND() =VLOOKUP(D11,IF(C11=$K$8,$K$9:$L$15,IF(C11=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E11)*50 =$B$1.33 =MAX(0,$B$1-E11)*10 =F11+H11-G11 =K10+M10 60 0.15 129 =RAND() =VLOOKUP(B12,$K$4:$L$6,2) =RAND() =VLOOKUP(D12,IF(C12=$K$8,$K$9:$L$15,IF(C12=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E12)*50 =$B$1*33 =MAX(0,$B$1-E12) 10 =F12+H12-G12 =K11+M11 70 0.2 13 10 =RAND() =VLOOKUP(B13,$K$4:$L$6,2) =RAND() =VLOOKUP(D13,IF(C13=$K$8,$K$9:$L$15,IF(C13=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E13)*50 =$B$1*33 =MAX(0,$B$1-E13)*10 =F13+H13-G13 =K12+M12 80 0.35 14 11 =RANDO) =VLOOKUP(B14,$K$4:$L$6,2) =RAND() =VLOOKUP(D14,IF(C14=$K$8,$K$9:$L$15,1F(C14=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E14)*50 -$B$1.33 =MAX(0,$B$1-E14) 10 =F14+H14-G14 =K13+M13 90 0.15 15 12 =RAND() =VLOOKUP(B15,$K$4:$L$6,2) =RAND() =VLOOKUP(D15, IF(C15-$K$8,$K$9:$L$15,IF(C15-$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E15)*50 =$B$1*33 =MAX(0,$B$1-E15)*10 =F15+H15-G15 =K14+M14 100 0.07 16 13 =RAND() =VLOOKUP(B16,$K$4:$L$6,2) =RAND() =VLOOKUP(D16,IF(C16=$K$8,$K$9:$L$15,1F(C16=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E16)*50 =$B$1.33 =MAX(0,$B$1-E16)*10 =F16+H16-G16 17 14 =RAND() =VLOOKUP(B17,$K$4:$L$6,2) =RAND() =VLOOKUP(D17,1F(C17=$K$8,$K$9:$L$15,1F(C17=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E17)*50 =$B$1*33 =MAX(0,$B$1-E17)*10 =F17+H17-G17 Fair Demand Prob 18 15 =RAND() =VLOOKUP(B18,$K$4:$L$6,2) =RAND() =VLOOKUP(D18,IF(C18=$K$8,$K$9:$L$15,IF(C18=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E18)*50 =$B$1.33 =MAX(0,$B$1-E18)*10 =F18+H18-G18 0 40 0.1 19 16 =RAND() =VLOOKUP(B19,$K$4:$L$6,2) =RAND() =VLOOKUP(D19,IF(C19-$K$8,$K$9:$L$15,IF(C19=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E19)*50 =$B$1*33 =MAX(0,$B$1-E19)*10 =F19+H19-G19 =K18+M18 50 0.18 20 17 =RAND() =VLOOKUP(B20,$K$4:$L$6,2) =RAND() =VLOOKUP(D20,1F(C20=$K$8,$K$9:$L$15,1F(C20-$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E20)*50 =$B$1*33 =MAX(0,$B$1-E20)*10 =F20+H20-G20 =K19+M19 60 0.4 21 18 =RAND() =VLOOKUP(B21,$K$4:$L$6,2) =RAND() =VLOOKUP(D21,IF(C21=$K$8,$K$9:$L$15,IF(C21=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E21)*50 =$$L$=$$$KK$$$))2 =$B$1*33 =MAX(0,$B$1-E21) 10 =F21+H21-G21 =K20+M20 70 0.2 22 19 =RAND() =VLOOKUP(B22,$K$4:$L$6,2) =RAND() =VLOOKUP(D22,IF(C22=$K$8,$K$9:$L$15,IF(C22=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E22)*50 =$B$1*33 =MAX(0,$B$1-E22)* 10 =F22+H22-G22 =K21+M21 80 0.08 23 20 =RAND() =VLOOKUP(B23,$K$4:$L$6,2) =RAND() =VLOOKUP(D23,IF(C23=$K$8,$K$9:$L$15,IF(C23=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E23)*50 =$B$1*33 =MAX(0,$B$1-E23)*10 =F23+H23-G23 =K22+M22 90 0.04 24 21 =RAND() =VLOOKUP(B24,$K$4:$L$6,2) =RAND() =VLOOKUP(D24, IF(C24=$K$8,$K$9:$L$15,IF(C24=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E24)*50 =$B$1*33 =MAX(0,$B$1-E24)*10 =F24+H24-G24 25 22 =RANDO) =VLOOKUP(B25,$K$4:$L$6,2) =RAND() =VLOOKUP(D25,IF(C25=$K$8,$K$9:$L$15,IF(C25=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E25)*50 =$B$1.33 =MAX(0,$B$1-E25)* 10 =F25+H25-G25 Poor Demand Prob 26 23 =RAND() =VLOOKUP(B26,$K$4:$L$6,2) =RAND() =VLOOKUP(D26,IF(C26=$K$8,$K$9:$L$15,1F(C26=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E26)*50=$B$1*33 =MAX(0,$B$1-E26)*10 =F26+H26-G26 $( 0 40 0.44 27 24 =RAND() =VLOOKUP(B27,$K$4:$L$6,2) =RAND() =VLOOKUP(D27,IF(C27=$K$8,$K$9:$L$15,1F(C27=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E27)*50 =$B$1.33 =MAX(0,$B$1-E27)*10 =F27+H27-G27 =K26+M26 50 0.22 28 25 =RAND() =VLOOKUP(B28,$K$4:$L$6,2) =RAND() =VLOOKUP(D28,IF(C28=$K$8,$K$9:$L$15,IF(C28=$K$17,$K$18:$L$23,$K$26:$L$30)),2) =MIN($B$1,E28)*50 =$B$1*33 =MAX(0,$B$1-E28)* 10 =F28+H28-628 =K27+M27 60 0.16 29 26 =RANDO) =VLOOKUP(B29,$K$4:$L$6,2) =RAND() =VLOOKUP(D29,IF(C29=$K$8,$K$9:$L$15,IF(C29=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E29)*50 =$B$1.33 =MAX(0,$B$1-E29)*10 =F29+H29-G29 =K28+M28 70 0.12 30 27 =RAND() =VLOOKUP(B30,$K$4:$L$6,2) =RAND() =VLOOKUP(D30,1F(C30=$K$8,$K$9:$L$15,IF(C30-$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E30)*50 =$B$1.33 =MAX(0,$B$1-E30) 10 =F30+H30-G30 $=K$=K$$$B, =K29+M29 80 0.06 43 40 =RANDO) =VLOOKUP(B43,$K$4:$L$6,2) =RAND() =VLOOKUP(D43,IF(C43=$K$8,$K$9:$L$15,IF(C43=$K$17,$K$18:$L$23,$K$26:$L$30)),2)=MIN($B$1,E43)*50 =$B$1*33 =MAX(0,$B$1-E43)*10 =F43+H43-643 44 Average =AVERAGE(14:14 N o P 1 2 Order size =144 3 4 5 0 00 N O uw 40 50 60 6 7 8 9 10 70 80 90 100 Data Table ? X x Row input cell: Column input cell: B11 OK Cancel Question 2. A classical inventory problem concerns the purchase and sale of newspapers. The paper seller buys the papers for 1.5 Halalas each and sells them for 3 Riyals each. Newspapers not sold at the end of the day are sold as scrap for 30 Halalas each. Newspapers can be purchased in bundles of 10. Thus, the paper seller can buy 50, 60, and so on. There are three types of Newsday's, good, fair, and poor with probabilities of 0.30, 0.45, and 0.25, respectively. The distribution of papers demanded on each of these days is given in table. The problem is to determine the total profit. This will be accomplished by simulating demands for 30 days and recording profits from sales each day. The distribution of demand for newspapers by type today is given in the following table: Demand 40 50 60 70 80 90 100 Good 0.02 0.06 0.20 0.15 0.18 0.32 0.07 Demand Probability Distribution Fair 0.12 0.16 0.35 0.25 0.08 0.04 0.00 Poor 0.33 0.26 0.18 0.15 0.08 0.00 0.00 Determine the optimal number of newspapers that a newspaper seller buys daily in order to achieve the highest profit. Simulate 30 days using EXCEL to find out what is required of whether the seller buys 80,70,60,50 newspapers per day. Note: Profits are calculated from the formula: P=R-C-L-S Where the symbols mean: (Profits) P = Profit (Total Sales Amount) R = Revenue from sales (Cost of newspapers) C = Cost of newspapers (Lost Profits from Not Fulfilling Order) (Refunded Amount from Selling Remaining Newspapers) L = Lost profit from excess demand S = salvage from sale of scrap papers