please use Inverse Function Theorem and Invertibility Requirement (below) to solve this question.

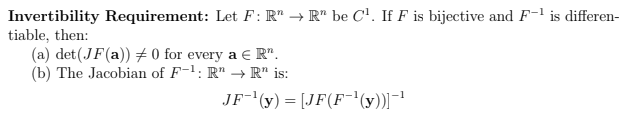
3. (6 points) Let f: R3 - R- be f(x, y) = (ex (y? -1), -yet) (a) Prove that f is not bijective. (Hint: Is (0, 0) in the range of f? Justify your claim.) (b) Prove that for every (x, y) ( R', there is an open set U containing (r, y) such that flu : U - f(U) is bijective. (c) Let g: f(U) - U be the inverse of flu : U - f(U). Find Jg(f(x, y)) for (r, y) E U.\fThe Inverse Function Theorem: Let F: U C R" - R" be a C function, where U C R" is open. Let a c U. If det(JF(a)) # 0, then there exists an open set V C U with a E V such that the restricted function Fv: V - F(V) is bijective. Moreover, its inverse (Fv) : F(V) - V is Cl