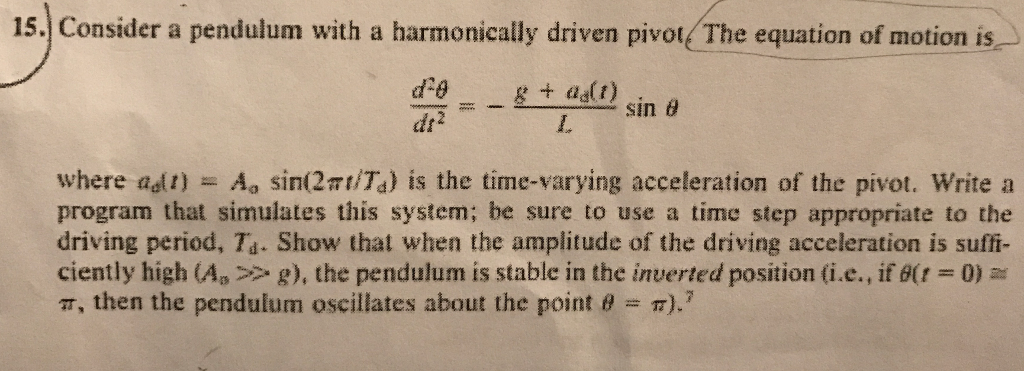
Please use Pend code below:

% Simple Pendulum solved by Euler's method with out small angle approximation clear; help pendE theta = 10*pi/180; theta_dot = 0; tau = 0.1; g_l = 1; nstep = 300; time = 0;

for istep =1:nstep t_plot(istep) = time; th_plot(istep) = theta; acc = - g_l*sin(theta); theta_dot = theta_dot + acc*tau; theta = theta + theta_dot*tau; %Cromer step time = time + tau; end

plot(t_plot, th_plot) xlabel('Time') ylabel('Theta') grid

1S. Consider a pendulum with a harmonically driven pivot The equation of motion is L. where adl)-A, sin(21/T) is the time-varying acceleration of the pivot, write a program that simulates this system; be sure to use a time step appropriate to the driving period, Ts. Show that when the amplitude of the driving acceleration is suffi- ciently high (An >> g), the pendulum is stable in the inverted position (i.e., if6(f = 0) r, then the pendulum oscillates about the point t 7