Please use python Language to solve part b) and solution in part a) has been posted.

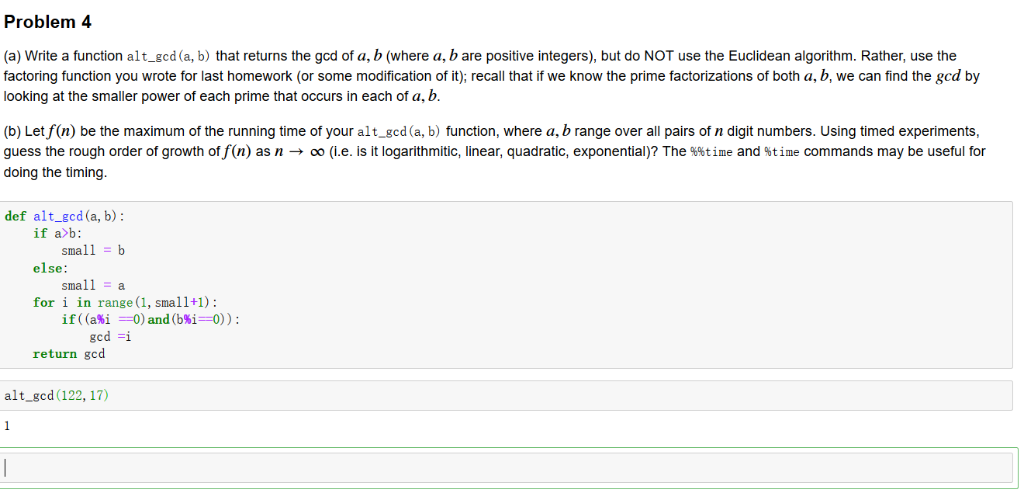
Problem 4 (a) Write a function alt_gcd (a, b) that returns the gcd of a, b (where a, b are positive integers), but do NOT use the Euclidean algorithm. Rather, use the factoring function you wrote for last homework (or some modification of it); recall that if we know the prime factorizations of both a, b, we can find the gcd by looking at the smaller power of each prime that occurs in each of a, b. (b) Let f(n) be the maximum of the running time of your alt_gcd(a, b) function, where a, b range over all pairs of n digit numbers. Using timed experiments, guess the rough order of growth of n as n oo le. is it logarithmitic linear quadratic, exponential ? The %%time and %time commands may be useful for doing the timing. def alt_gcd (a, b) if a>b: small b else: small a for i in range (1, small+1) if((a% 0) and (Mi 0) ); return ged alt gcd (122,17) Problem 4 (a) Write a function alt_gcd (a, b) that returns the gcd of a, b (where a, b are positive integers), but do NOT use the Euclidean algorithm. Rather, use the factoring function you wrote for last homework (or some modification of it); recall that if we know the prime factorizations of both a, b, we can find the gcd by looking at the smaller power of each prime that occurs in each of a, b. (b) Let f(n) be the maximum of the running time of your alt_gcd(a, b) function, where a, b range over all pairs of n digit numbers. Using timed experiments, guess the rough order of growth of n as n oo le. is it logarithmitic linear quadratic, exponential ? The %%time and %time commands may be useful for doing the timing. def alt_gcd (a, b) if a>b: small b else: small a for i in range (1, small+1) if((a% 0) and (Mi 0) ); return ged alt gcd (122,17)