Please use python to answer.

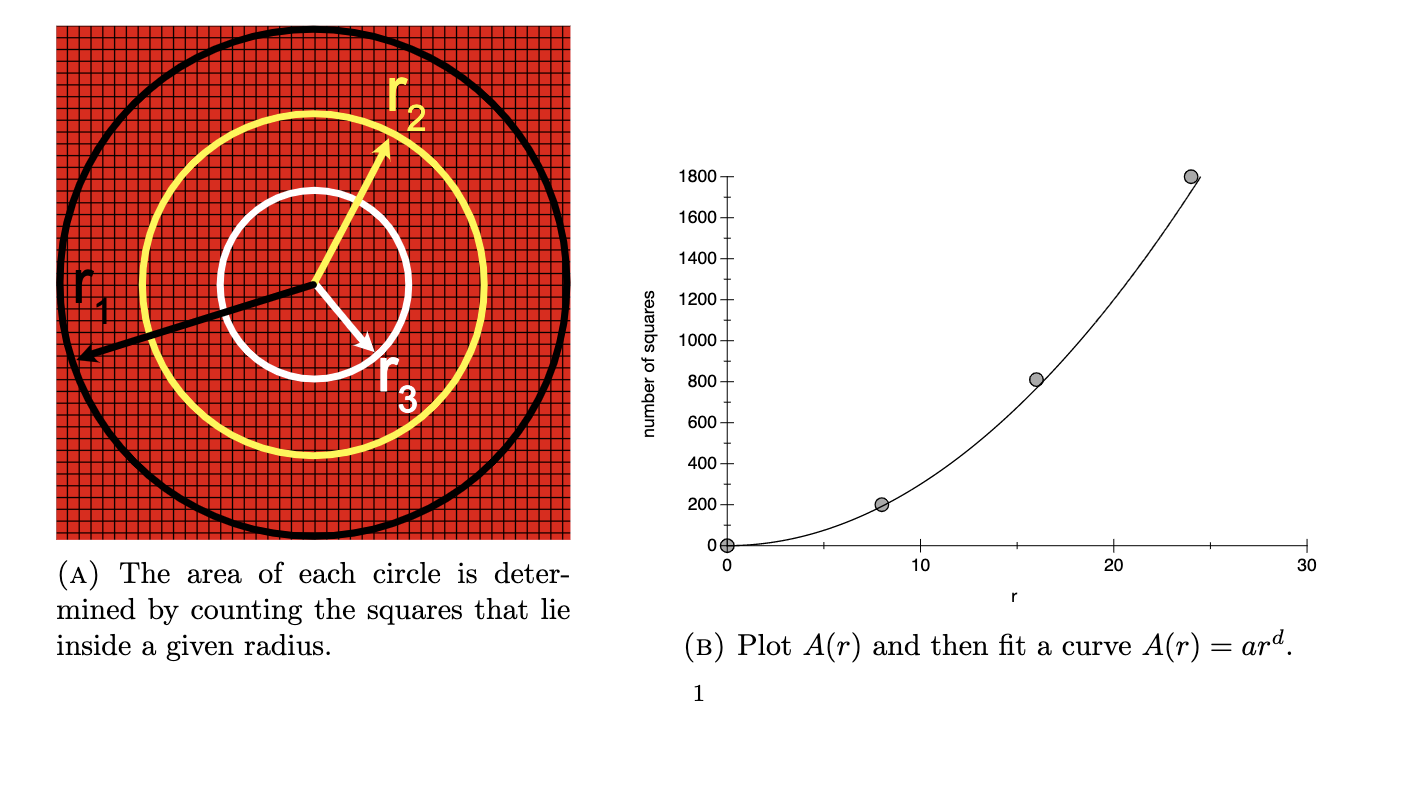
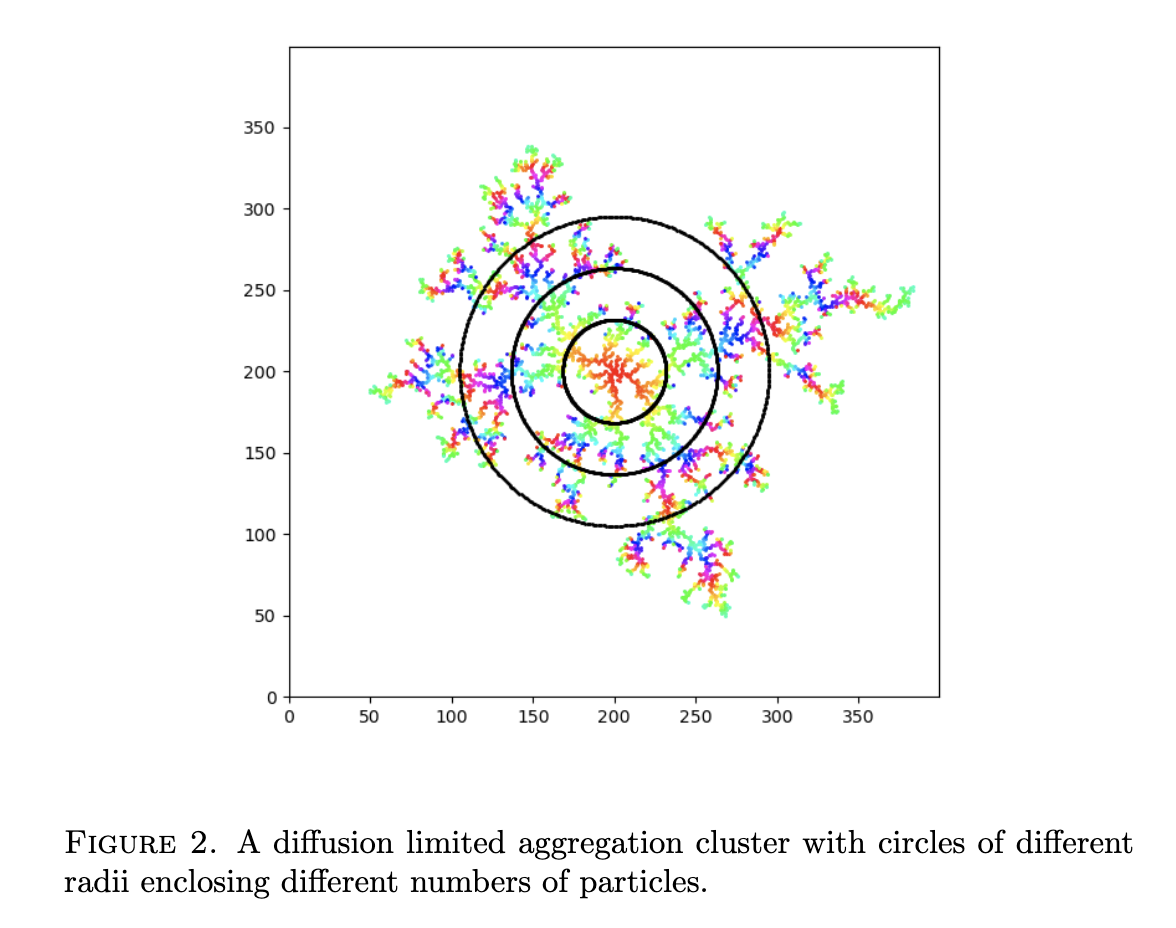
This assignment is to write a program to compute the fractal dimension of DLA clusters in 2 dimensions. There is a DLA python program shown at the last part has been sped up with numba and has some improvements in how the new particles are started off: they start off closer to the cluster and are distributed uniformly around the center. Rather than writing a single program, you will probably want to write multiple programs that save results in files that are read by subsequent programs. The basic procedure as following,

(1) Generate a cluster and count the number of particles within different radii.

(2) You will need to play with the cluster size and also chose a maximum radius that isnt too big. (3) Use scipy.optimize.curve fit() (or something else) to fit a function N(r) = ard to your data. (4) Repeat the above. Each time you will get a slightly different value of the fractal dimension d. Accumulate these measurements using the Datum class to determine the mean and standard deviation of d. (5) As a bonus, you can see how the size of the clusters affects the error in the final result.

DLA python program

import matplotlib.pyplot as plt import numpy as np import random import colorsys import numba import time #--------------------------------------- @numba.jit(nopython=True) def hasFixedNeighbor(x,y, Nx,Ny, stuck): """returns True if x,y is next to a site occupied by a particle that already got stuck. The box size, Nx,Ny is needed to implement periodic boundary conditions. stuck[i,j] = 0 if no particle is stuck on site i,j stuck[i,j] > 0 if a particle is stuck on site i,j. The value indicates the order of particles getting stuck (first particle 1, second particle 2, etc) """ for dx in range(-1,2): for dy in range(-1,2): if stuck[ (x+dx)%Nx, (y+dy)%Ny ] != 0: return True return False #--------------------------------------- @numba.jit(nopython=True) def update(s, Nstuck): (Nx,Ny) = (len(s),len(s[0])) (x,y) = ( 0, 0 ) # random walker starts at the edge of the box if random.randint(0,1): x = random.randint(0,Nx) else: y = random.randint(0,Ny) while True: r = random.randint(0,3) if r == 0: x = (x+1)%Nx elif r == 1: x = (x-1)%Nx elif r == 2: y = (y+1)%Ny elif r == 3: y = (y-1)%Ny if hasFixedNeighbor(x,y, Nx,Ny, s): Nstuck += 1 s[x,y] = Nstuck break return (x,y,Nstuck) ######################################################### (Nx,Ny)=(400,400) # size of box Nstuck = 1 # number of particles stuck so far

# initialize the array of stuck particles, with one at the center of the box stuck = np.zeros((Nx,Ny),dtype=int) stuck[ int(Nx/2), int(Ny/2)] = Nstuck

plt.axes().set_aspect('equal') plt.xlim(0,Nx-1) plt.ylim(0,Ny-1) plt.plot( int(Nx/2), int(Ny/2), 'r.')

x0,y0 = int(Nx/2), int(Ny/2) r0 = x0 - 10 sum_t = 0.0 for i in range(2000000): t0 = time.time() (x,y,Nstuck) = update( stuck, Nstuck) sum_t += time.time()-t0 #print(Nstuck,time.time()-t0) new_color = colorsys.hsv_to_rgb( (Nstuck/2000.0)%1 , 1,1) plt.plot(x,y,'.', color=new_color,markersize=2)

r = ( (x-x0)**2 + (y-y0)**2 )**0.5 - 3 if (x-x0)**2 + (y-y0)**2 >= r0**2: print((x-x0)**2 + (y-y0)**2,r0**2) break

x,y = x0 + r * np.cos( 2*np.pi*random.random() ), y0 + r * np.sin( 2*np.pi*random.random() ) ##### n = 600 r0 = 0.5*r0 for i in range(n): x,y = x0 + r0 * np.cos( 2*np.pi*i ), y0 + r0 * np.sin( 2*np.pi*i ) plt.plot(x,y,'k.',markersize=2) x,y = x0 + (2*r0/3) * np.cos( 2*np.pi*i ), y0 + (2*r0/3) * np.sin( 2*np.pi*i ) plt.plot(x,y,'k.',markersize=2) x,y = x0 + (r0/3) * np.cos( 2*np.pi*i ), y0 + (r0/3) * np.sin( 2*np.pi*i ) plt.plot(x,y,'k.',markersize=2) plt.show()

One way of looking at the dimensionality of an object is to examine how the "amount inside scales with the linear dimension of the object. For example, we know the area of a circle is given by A = r2. As shown in Fig. 1, one could count the squares inside a set of circles and plot the number vs r. Then by fitting a function A(r) = ard to the data points you could determine an approximate formula for the area, and the exponent d gives the dimensionality of the circle. It should come out very close to 2, but of course there will be some error from counting or not counting squares that don't quite fit the circle. 2 1800 1600 1400 1200 1000 number of squares 800 3 600 200 00 0 10 20 30 r (A) The area of each circle is deter- mined by counting the squares that lie inside a given radius. (B) Plot A(r) and then fit a curve A(r) = ard. = 1 350 300 250 200- 150 100 50 0 50 100 150 200 250 300 350 FIGURE 2. A diffusion limited aggregation cluster with circles of different radii enclosing different numbers of particles. Now consider the diffusion limited aggregation (DLA) simulations we have worked with. We can apply the same area law method outlined above to a DLA cluster, counting the number of stuck particles inside a given radius. You can see from Fig. 2 that the voids in the cluster mean the number of particles will grow more slowly than the number of grid sites shown in Fig. 2. Fitting a function N(r) ard to the number of particles vs r, the number d is called the fractal dimension of the cluster. Since the cluster has a finite size, one needs to be careful to use circles that are small enough that they don't simply include a lot of empty space beyond the cluster dimensions. One way of looking at the dimensionality of an object is to examine how the "amount inside scales with the linear dimension of the object. For example, we know the area of a circle is given by A = r2. As shown in Fig. 1, one could count the squares inside a set of circles and plot the number vs r. Then by fitting a function A(r) = ard to the data points you could determine an approximate formula for the area, and the exponent d gives the dimensionality of the circle. It should come out very close to 2, but of course there will be some error from counting or not counting squares that don't quite fit the circle. 2 1800 1600 1400 1200 1000 number of squares 800 3 600 200 00 0 10 20 30 r (A) The area of each circle is deter- mined by counting the squares that lie inside a given radius. (B) Plot A(r) and then fit a curve A(r) = ard. = 1 350 300 250 200- 150 100 50 0 50 100 150 200 250 300 350 FIGURE 2. A diffusion limited aggregation cluster with circles of different radii enclosing different numbers of particles. Now consider the diffusion limited aggregation (DLA) simulations we have worked with. We can apply the same area law method outlined above to a DLA cluster, counting the number of stuck particles inside a given radius. You can see from Fig. 2 that the voids in the cluster mean the number of particles will grow more slowly than the number of grid sites shown in Fig. 2. Fitting a function N(r) ard to the number of particles vs r, the number d is called the fractal dimension of the cluster. Since the cluster has a finite size, one needs to be careful to use circles that are small enough that they don't simply include a lot of empty space beyond the cluster dimensions