Please write it as a demonstration in a white sheet

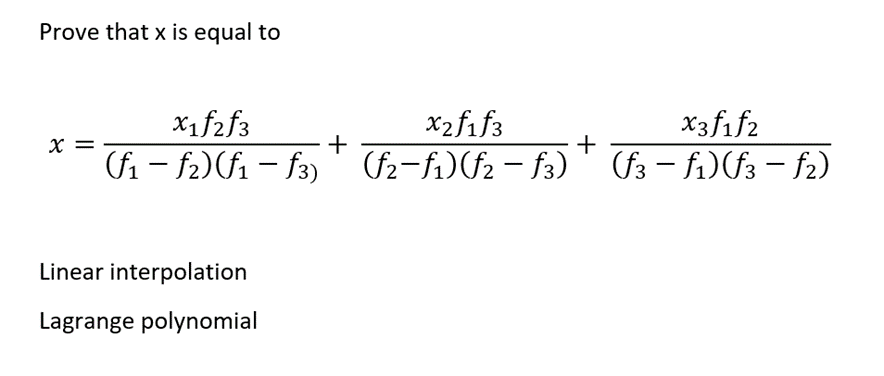
Prove that x is equal to x=(f1f2)(f1f3)x1f2f3+(f2f1)(f2f3)x2f1f3+(f3f1)(f3f2)x3f1f2 Linear interpolation Lagrange polynomial The inverse quadratic interpolation algorithm is defined by the recurrence relation xn+1=(fn2fn1)(fn2fn)fn1fnxn2+(fn1fn2)(fn1fn1)fn2fnxn1+(fnfn2)(fnfn1)fn2xn, where fk=f(xk). As can be seen from the recurrence relation, this method requires three initial values, x0,x1 and x2