Plot the following function in MATLAB:

y = f(x) = ln(x^4) - 0.7

and convince yourself that f(x) has a unique positive root.

Determine this root using the method of false-position, with the initial bracketing interval [xl, xu], and the stopping criterion es as input in MATLAB.

Note: es denotes the maximum allowable approximate absolute percent relative error in the root

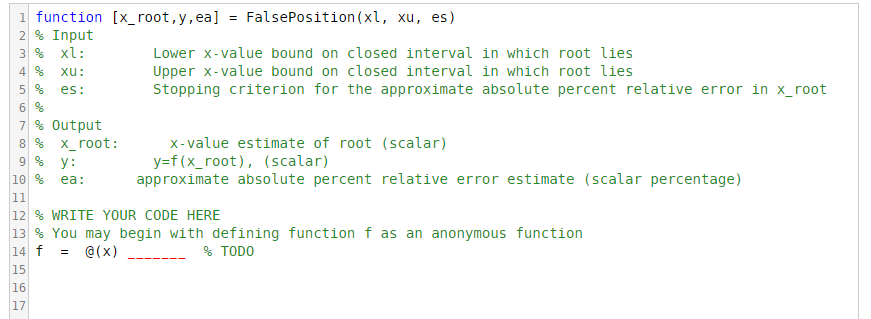
1 function [s_root , y, ea] = FalsePosition ( xl, xu, es) 2% Input 31% xl: 41% xu : 51% es: Lower x-value bound onclosed interval in which root lies Upper x-value bound on closed interval in which root lies Stopping criterion for the approximate absolute percent relative error in x_root 71 % output 8% xroot: 9/ % x-value estimate of root (scalar) y f (x_root), (scalar) - approximate absolute percent relative error estimate (scalar percentage) 12% WRITE YOUR CODE HERE 13% You may begin with defining function f as an anonymous function 14 f = @(x) 15 16 17 % TODO