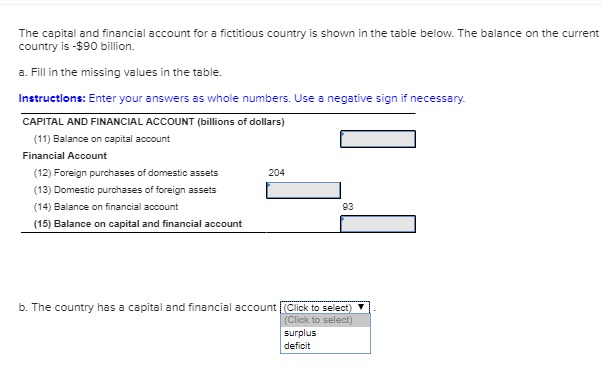
Question: Poisson sampling. Let {X(t)} be a continuous-time Markov chain with stationary distribution pi . We sample the chain at times given by an independent Poisson
Poisson sampling.
Let {X(t)} be a continuous-time Markov chain with stationary distribution \pi . We sample the chain at times given by an independent Poisson process: let N(t) be a Poisson process with rate \alpha , independent of the Markov chain, and define Yn= X(Tn +), the value taken by X immediately after the epoch Tnof the nth arrival of N. Show that {Yn} is a discrete-time Markov chain with the same stationary distribution as X.

Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


