Polynomial root calculation

Create a C program using loops (for, while, if, etc)

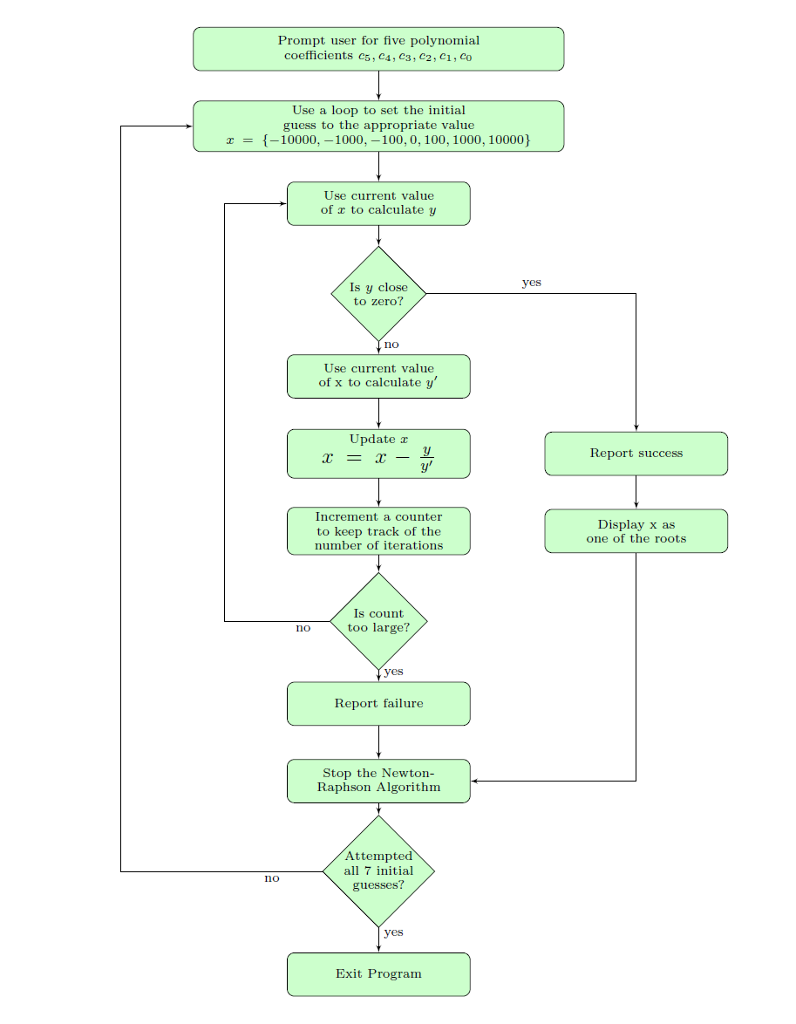
2.1 Newton-Raphson Algorithm: Write a program that prompts the user to input the coefficients cs, c4, C3, c2, ci, co of a 5-order polynomial The 5ih order polynomial has the form We know that the first derivative of y with respect tois d.r We can use this information to find the roots of the polynomial. The basic idea, in the Newton-Raphson mcthod, is as follows: (a) Given an initial guess , and polynomial cocfficients c, calculate y (b) Check to see if y is close enough to zero, i.c. within some small tolerance close to zero (i) If so then terminate. Algorithm has converged! (ii) If not then continue (c) Usc the current value of a to calculate y' (d) Create a new guess for x using the update formula x = x- (e) Increment a counter to count the number of algorithm iterations (f) Check to see if the number of iterations has exceeded a predetermined count limit (say 500) y' (i) If so then terminatc. Algorith (ii) If not then return to step a has failed! We would like to use 7 different initial guesses to test the Newton-Raphson algorithm; XInitalGuess -10000, -1000,-100, 0, 100, 1000, 10000) Thus your code will need to loop around the Newton-Raphson algorithm 7 times, once for cach initial guess This same information is described in the flow chart below: 2.1 Newton-Raphson Algorithm: Write a program that prompts the user to input the coefficients cs, c4, C3, c2, ci, co of a 5-order polynomial The 5ih order polynomial has the form We know that the first derivative of y with respect tois d.r We can use this information to find the roots of the polynomial. The basic idea, in the Newton-Raphson mcthod, is as follows: (a) Given an initial guess , and polynomial cocfficients c, calculate y (b) Check to see if y is close enough to zero, i.c. within some small tolerance close to zero (i) If so then terminate. Algorithm has converged! (ii) If not then continue (c) Usc the current value of a to calculate y' (d) Create a new guess for x using the update formula x = x- (e) Increment a counter to count the number of algorithm iterations (f) Check to see if the number of iterations has exceeded a predetermined count limit (say 500) y' (i) If so then terminatc. Algorith (ii) If not then return to step a has failed! We would like to use 7 different initial guesses to test the Newton-Raphson algorithm; XInitalGuess -10000, -1000,-100, 0, 100, 1000, 10000) Thus your code will need to loop around the Newton-Raphson algorithm 7 times, once for cach initial guess This same information is described in the flow chart below