Problem 2: Polynomial Root Calculation Problem Description:

Engineers often need to calculate the roots to a given polynomial. For low order polynomials these computations can be done by hand. For higher order polynomials these calculations can be cumbersome, if not impossible, without a computer. One method of finding real roots of a polynomial is the Newton-Raphson algorithm.

In this homework we will write a program that uses the Newton-Raphson method for calculating the roots of a polynomial. Although our program will not be able to solve for complex roots, it will be able to calculate real roots; maybe later we will upgrade the routine to include complex roots. Since it is possible that the polynomial roots are all complex, i.e. no real roots at all, or it may be that the Newton-Raphson routine fails to converge.

(a) Newton-Raphson Algorithm:

Write a C program that prompts the user to input a set of 5th-order polynomial coefficients, of the form c5; c4; c3; c2; c1; c0. Also, the user will need to submit an initial value of x which serves as the starting condition of the Newton-Raphson algorithm.

The 5th-order polynomial has the form y = c5 x5 + c4 x 4 + c3 x 3 + c2 x 2 + c1 x + c0

We know that the first derivative of y with respect to x is 5 c5 x 4 + 4 c4 x 3 + 3 c3 x 2 + 2 c2 x + c1

We can use this information to find the roots of the polynomial. The basic idea, in the Newton-Raphson method, is as follows:

(a) Given an initial guess (or the updated value) x, and polynomial coefficients c,

calculate y (b) Check to see if y is close enough to zero, i.e. within some small tolerance close to zero.

(i) If so then terminate. Algorithm has converged! (ii) If not then continue

(c) Use the current value of x to calculate

(d) Create a new guess for x using the update formulate x = x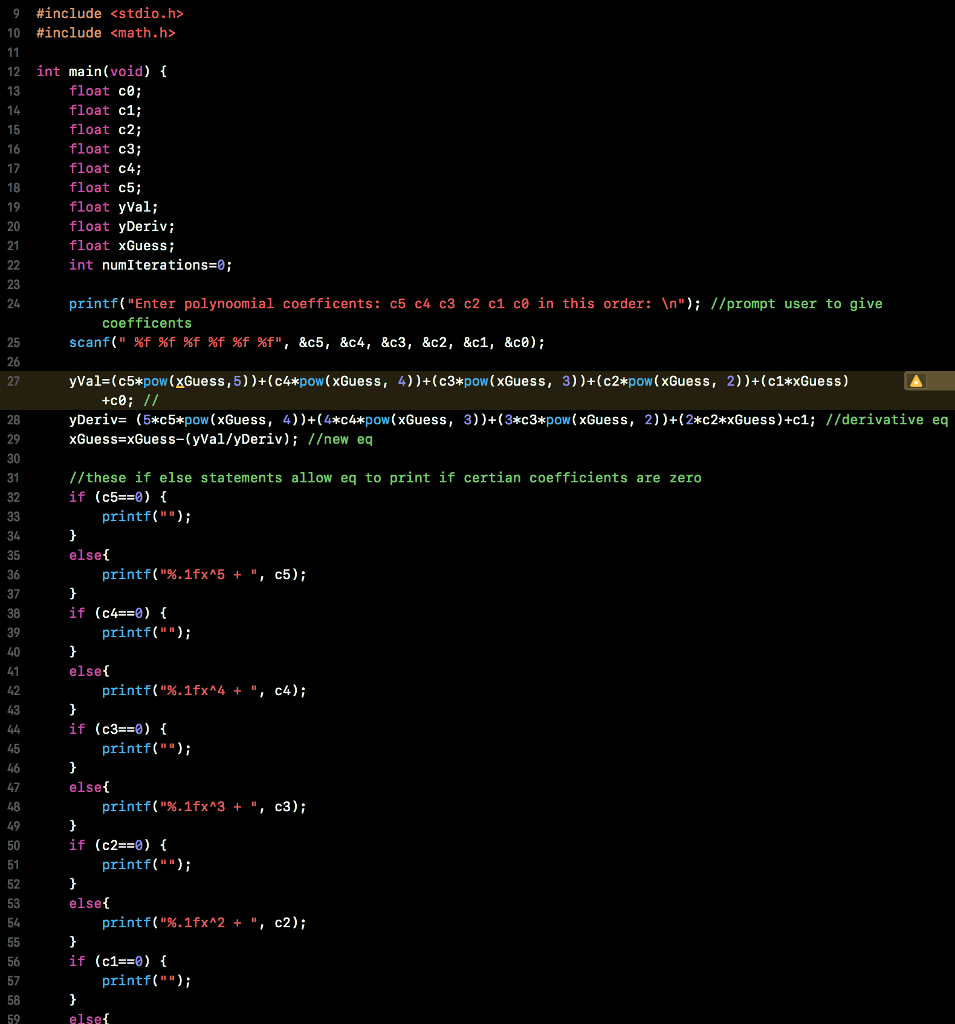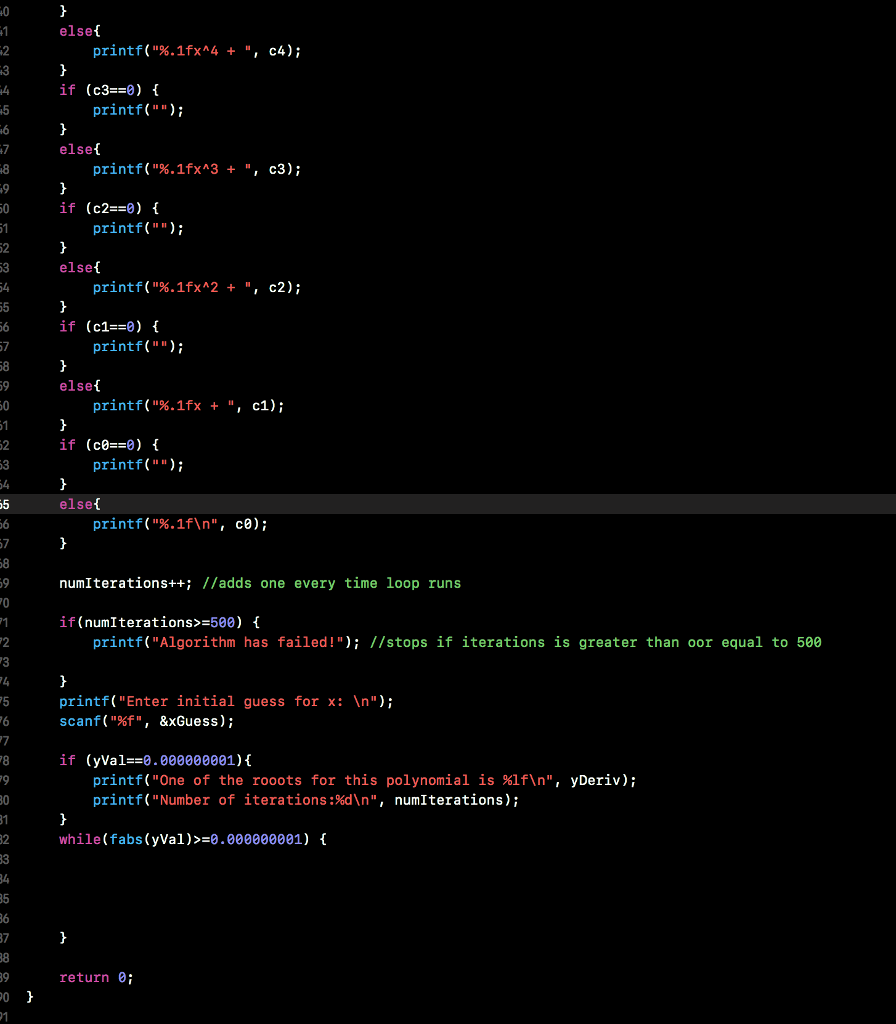This is the code I have so far for the problem I just need help doing a loop for the root and fixing my iterations. Please do not use complicated coding because I am taking an intro course and will not understand. Thank you!!

#include 10 #include 12 int main (void) float c0; float c1; float c2; float c3; float c4; float c5; float yVal; float yDeriv; float xGuess int numIterations 0; 15 17 20 21 23 printf("Enter polynoomial coefficents c5 c4 c3 c2 c1 c0 in this order: "); //prompt user to give coefficents 25 26 27 yVal-(c5pow (xGuess,5))+(c4*pow( xGuess, 4))+(c3*pow (xGuess, 3))+(c2xpow( xGuess, 2))+(c1*xGuess) yDeriv= (5%c 5*pow(xGuess, 4))+(4*c4*pow(xGuess, xGuess-xGuess-(yVal/yDeriv); /ew edq 3))+(3*c3*pow(xGuess, 2))+(22*XGuess)+c1; //derivative 28 29 30 31 eq //these if else statements allow eq to print if certian coefficients are zero if (c5 0) printf(""); 34 35 36 37 38 39 elset printf("%. 1fxa5 + ", c5); if (c4 0) printf(""); elset printf("%. 1fx4 + ", c4); if (c3 0) printf("); 47 elset printf("%. 1fxng + ", c3 ); 49 50 if (c2--0) printf(" "); 52 53 elset printf("%. 1#x^2 + ", c2); if (c1 0) 56 57 printf(") 59 elsef