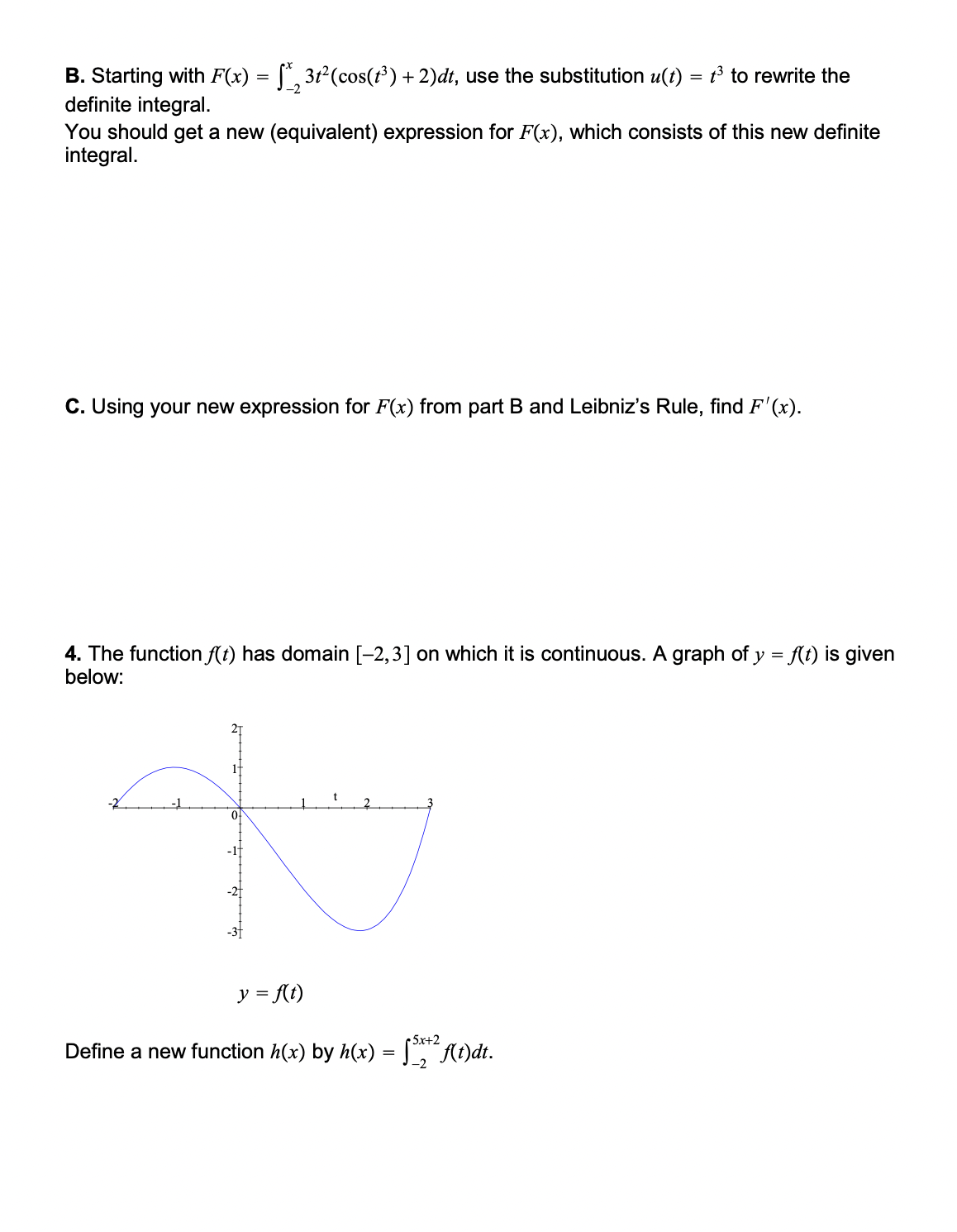
Practice Analyzing Functions Defined by Definite Integrals 1. Practice finding the derivatives of functions that are defined by definite integrals. A. Let g(u) = ]; 2 dx. Then de = B. Find d [ -cos(32x) (31 + 1)dt. C. Let F(x) = _ cos( TS ) ds. Find F'(-1/4). 2. The cost of producing x units of a certain commodity is given by P(x) = 1000 + J. MC(s) ds, where P is in dollars and M(x) is marginal cost in dollars per unit. A. Suppose the marginal cost at a production level of 500 units is $10 per unit, and the cost of producing 500 units is $12,000 (that is, M(500) = 10 and P(500) = 12000). Use a tangent line approximation to estimate the cost of producing only 497 units.B. Suppose the production schedule is such that the company produces ve units each day. That is, the number of units produced is x = 5:, where t is in days, and t = 0 corresponds to the beginning of production. Write an equation for the cost of production P as a function of time t. C. Use your equation for P(t) from part B to nd %. Be sure to indicate units and describe what % represents, practically speaking. 3. Let F(x) = j; 3:2(0050'3) + 2m. A. Using the First Fundamental Theorem of Calculus, find F'(x). (Yes, this is as easy as it seems.) B. Starting with F(x) = ], 312(cos(13) + 2)dt, use the substitution u(t) = 13 to rewrite the definite integral. You should get a new (equivalent) expression for F(x), which consists of this new definite integral. C. Using your new expression for F(x) from part B and Leibniz's Rule, find F' (x). 4. The function f(t) has domain [-2,3] on which it is continuous. A graph of y = f(t) is given below: -2 y = f(t) Define a new function h(x) by h(x) = ]_,f(t)dt.A. What is the domain of h(x) (that is, on which x values is the function h(x) defined)? B. Find h'(). C. At what x value(s) does the function h(x) attain a relative maximum