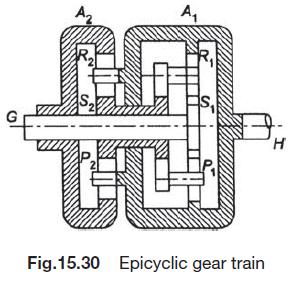
An epicyclic gear train is shown in Fig.15.30. The main driving shaft G has a gear S, integrally mounted and driving the internal gear 4, on the casing through two intermediate gears P, mounted on either side. The gears P, are free to revolve on arms R, which are integral with gear S, which in turn drives the internal gear A, on another casing through two gears P2. The driven shaft H is integral with the casing carrying the internal gear A, and arms R, on which the gears P are free to rotate. The casing A, and gear S, are free to rotate on shaft G. Calculate the speed of shaft H when G rotates at 1000 rpm anticlockwise when (a) A, is stationary; (b) 4, rotates at 500 rpm clockwise. The number of teeth on gears are: S = S = 30, A = A = 90. A Fig.15.30 Epicyclic gear train H