(Primal-Dual path following algorithm for convex quadratic programming)

Consider he optimization problem

minimize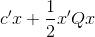

subject to Ax = b

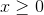
where Q is an n x n positive semidefinite matrix(that is, x'Qx >= 0 for all x).

We introduce the logarithmic barrier problem:

minimize

subject to Ax = b.

The associate Karush-Kuhn-Tucker optimality conditions are

Ax(?) = b,

-Qx(?) + A'p(?) + s(?) = c

X(?)S(?)e = e?,

where X(?) = diag(x₁(?), ..., x_n(?)) and S(?) = diag(s₁(?), ..., s_n(?)).

Question:

(a) Show that a Newton Direction can be found by solving the following system of equations

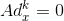
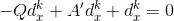
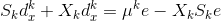
(b) Show that the solution to the system of equations in part (a) is given by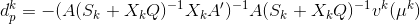

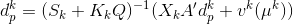
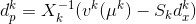
with v^k(?^k) = ?^ke - X_kS_ke.

(c) Based on part (b) develop a primal-dual path following interior point algorithm. (You do not ned to prove convergence!!!!)

+ ,for + ,for