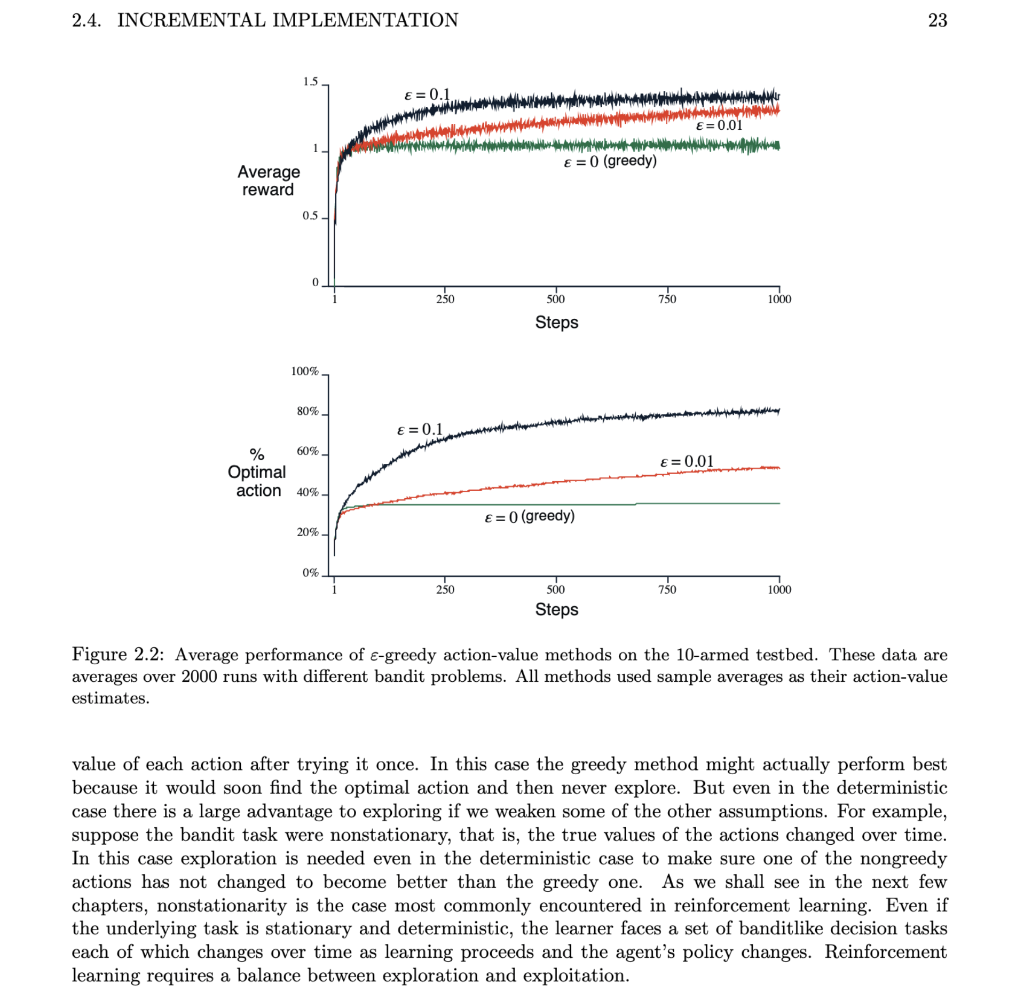
Problem 1 (24 marks) Re-implement in Python the results presented in Figure 2.2 of the Sutton & Barto book comparing a greedy method with two e-greedy methods ( = 0.01 and = 0.1), on the 10-armed testbed, and present your code and results. Include a discussion of the exploration - exploitation dilemma in relation to your findings. 2.4. INCREMENTAL IMPLEMENTATION 23 1.5 E = 0.01 E = 0 (greedy) Average reward 0.5 0 250 n 750 1000 500 Steps 100% 80% E = 0.1 E=0.01 % 60% Optimal action 40% E = 0 (greedy) 20% 0% 250 750 1000 500 Steps Figure 2.2: Average performance of e-greedy action-value methods on the 10-armed testbed. These data are averages over 2000 runs with different bandit problems. All methods used sample averages as their action-value estimates. value of each action after trying it once. In this case the greedy method might actually perform best because it would soon find the optimal action and then never explore. But even in the deterministic case there is a large advantage to exploring if we weaken some of the other assumptions. For example, suppose the bandit task were nonstationary, that is, the true values of the actions changed over time. In this case exploration is needed even in the deterministic case to make sure one of the nongreedy actions has not changed to become better than the greedy one. As we shall see in the next few chapters, nonstationarity is the case most commonly encountered in reinforcement learning. Even if the underlying task is stationary and deterministic, the learner faces a set of banditlike decision tasks each of which changes over time as learning proceeds and the agent's policy changes. Reinforcement learning requires a balance between exploration and exploitation. Problem 1 (24 marks) Re-implement in Python the results presented in Figure 2.2 of the Sutton & Barto book comparing a greedy method with two e-greedy methods ( = 0.01 and = 0.1), on the 10-armed testbed, and present your code and results. Include a discussion of the exploration - exploitation dilemma in relation to your findings. 2.4. INCREMENTAL IMPLEMENTATION 23 1.5 E = 0.01 E = 0 (greedy) Average reward 0.5 0 250 n 750 1000 500 Steps 100% 80% E = 0.1 E=0.01 % 60% Optimal action 40% E = 0 (greedy) 20% 0% 250 750 1000 500 Steps Figure 2.2: Average performance of e-greedy action-value methods on the 10-armed testbed. These data are averages over 2000 runs with different bandit problems. All methods used sample averages as their action-value estimates. value of each action after trying it once. In this case the greedy method might actually perform best because it would soon find the optimal action and then never explore. But even in the deterministic case there is a large advantage to exploring if we weaken some of the other assumptions. For example, suppose the bandit task were nonstationary, that is, the true values of the actions changed over time. In this case exploration is needed even in the deterministic case to make sure one of the nongreedy actions has not changed to become better than the greedy one. As we shall see in the next few chapters, nonstationarity is the case most commonly encountered in reinforcement learning. Even if the underlying task is stationary and deterministic, the learner faces a set of banditlike decision tasks each of which changes over time as learning proceeds and the agent's policy changes. Reinforcement learning requires a balance between exploration and exploitation