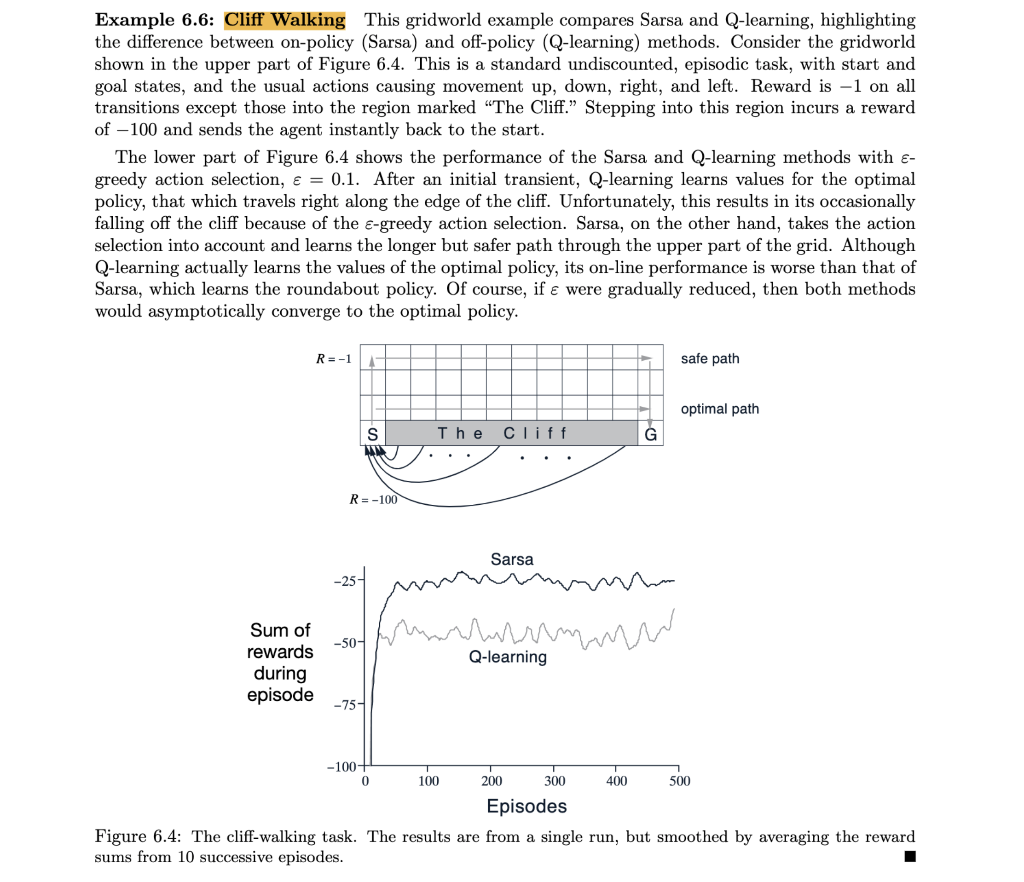
Problem 5 (30 marks) Re-implement in Python the results presented in Figure 6.4 of the Sutton & Barto book comparing SARSA and Q-learning in the cliff-walking task. Investigate the effect of choosing different values for the exploration parameter for both methods. Present your code and results. In your discussion clearly describe the main difference between SARSA and Q-learning in relation to your findings. Note: For this problem, use a = 0.1 and y = 1 for both algorithms. The "smoothing" that is mentioned in the caption of Figure 6.4 is a result of 1) averaging over 10 runs, and 2) plotting a moving average over the last 10 episodes. Example 6.6: Cliff Walking This gridworld example compares Sarsa and Q-learning, highlighting the difference between on-policy (Sarsa) and off-policy (Q-learning) methods. Consider the gridworld shown in the upper part of Figure 6.4. This is a standard undiscounted, episodic task, with start and goal states, and the usual actions causing movement up, down, right, and left. Reward is -1 on all transitions except those into the region marked "The Cliff." Stepping into this region incurs a reward of 100 and sends the agent instantly back to the start. The lower part of Figure 6.4 shows the performance of the Sarsa and Q-learning methods with e- greedy action selection, = 0.1. After an initial transient, Q-learning learns values for the optimal policy, that which travels right along the edge of the cliff. Unfortunately, this results in its occasionally falling off the cliff because of the e-greedy action selection. Sarsa, on the other hand, takes the action selection into account and learns the longer but safer path through the upper part of the grid. Although Q-learning actually learns the values of the optimal policy, its on-line performance is worse than that of Sarsa, which learns the roundabout policy. Of course, if were gradually reduced, then both methods would asymptotically converge to the optimal policy. R= -1 safe path optimal path S The Cliff G R = -100 Sarsa -25- mm -50- Sum of rewards during episode Q-learning -75- -100+ 0 100 300 200 400 500 Episodes Figure 6.4: The cliff-walking task. The results are from a single run, but smoothed by averaging the reward sums from 10 successive episodes. Problem 5 (30 marks) Re-implement in Python the results presented in Figure 6.4 of the Sutton & Barto book comparing SARSA and Q-learning in the cliff-walking task. Investigate the effect of choosing different values for the exploration parameter for both methods. Present your code and results. In your discussion clearly describe the main difference between SARSA and Q-learning in relation to your findings. Note: For this problem, use a = 0.1 and y = 1 for both algorithms. The "smoothing" that is mentioned in the caption of Figure 6.4 is a result of 1) averaging over 10 runs, and 2) plotting a moving average over the last 10 episodes. Example 6.6: Cliff Walking This gridworld example compares Sarsa and Q-learning, highlighting the difference between on-policy (Sarsa) and off-policy (Q-learning) methods. Consider the gridworld shown in the upper part of Figure 6.4. This is a standard undiscounted, episodic task, with start and goal states, and the usual actions causing movement up, down, right, and left. Reward is -1 on all transitions except those into the region marked "The Cliff." Stepping into this region incurs a reward of 100 and sends the agent instantly back to the start. The lower part of Figure 6.4 shows the performance of the Sarsa and Q-learning methods with e- greedy action selection, = 0.1. After an initial transient, Q-learning learns values for the optimal policy, that which travels right along the edge of the cliff. Unfortunately, this results in its occasionally falling off the cliff because of the e-greedy action selection. Sarsa, on the other hand, takes the action selection into account and learns the longer but safer path through the upper part of the grid. Although Q-learning actually learns the values of the optimal policy, its on-line performance is worse than that of Sarsa, which learns the roundabout policy. Of course, if were gradually reduced, then both methods would asymptotically converge to the optimal policy. R= -1 safe path optimal path S The Cliff G R = -100 Sarsa -25- mm -50- Sum of rewards during episode Q-learning -75- -100+ 0 100 300 200 400 500 Episodes Figure 6.4: The cliff-walking task. The results are from a single run, but smoothed by averaging the reward sums from 10 successive episodes