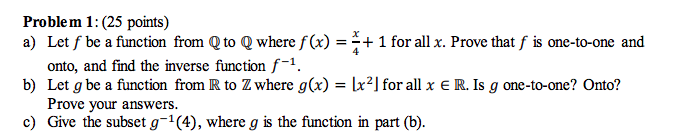
Problem 1: (25 points) a) Let f be a function from Q to Q where f(x) = + 1 for all x. Prove that f is one-to-one and onto, and find the inverse function f-1. b) Let g be a function from R to Z where g(x) = [x2] for all x E R. Is g one-to-one? Onto? Prove your answers. c) Give the subset g-1(4), where g is the function in part (b)