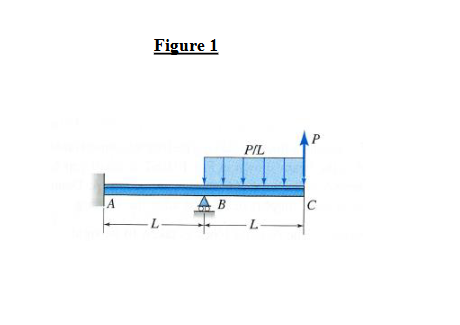
Problem #$1$: $(70$ points$)$ The beam ABC of length $2$L is fixed $($i$.$e$.$ clamped$)$ at point A and supported by a roller at B$,$ as shown in Figure $1($on the following page$).$ The beam is loaded by an upward concentrated force P at end C and by a uniform downward load of w$=$P$//$L over a length L of the span between points B and C$,$ as shown. In an x$-$y$-$z coordinate system $($not shown in the figure$)$ with origin at the centroid of the cross section, the positive x$-$direction measures horizontal distance to the right of point A$,$ and the positive y$-$direction measures vertical distances above the

centroid of the cross$-$section. The beam has a Young's modulus E E its cross section has a moment of inertia I$\_($zz$)$ about the z$-$axis. $($Express your results obtained below in terms of L$,$P$,$E and I$\_($zz$).)$

a$)$ Draw a free body diagram of the entire beam and write down the equilibrium equations for the entire beam. If the problem to find the reactions is statically determinate, then find the reactions. If the problem is statically indeterminate, then find the reactions in terms of the unknown couple exerted by the wall on the beam.

b$)$ Find the equations for the bending moment M$=$M$($x$)$ throughout the beam. If more than one cut is required, then denote the bending moment in each range $($of x $)$ by M$\_(1)($x$),$M$\_(2)($x$),$ etc. If the problem is statically indeterminate, then express the results in terms of the unknown couple exerted by the wall.

c$)$ Use the results from part b$)$ to find the equations for the vertical deflection v$=$v$($x$)$ throughout the beam in terms of constants of integration and any unknown reactions needed. If more than one cut is required, then denote the deflection in each range $($of x $)$ by v$\_(1)($x$),$v$\_(2)($x$),$ etc.

d$)$ Write down all the boundary conditions and matching conditions needed to determine all the unknown reactions $($if the problem is statically indeterminate$)$ and to completely determine the deflection in each range.

e$)$ Determine all the unknown reactions $($if the problem is statically indeterminate$)$ and completely determine the deflection in each range.

f$)$ Find the maximum deflection $($denoted by v$\_($AB$))$ between points A and B$,$ and determine the location $($denoted by x$\_($AB$))$ at which it occurs. $($Note: You should find x$\_($AB$)$ in terms of L$,$ only.$)$

Figure $1$