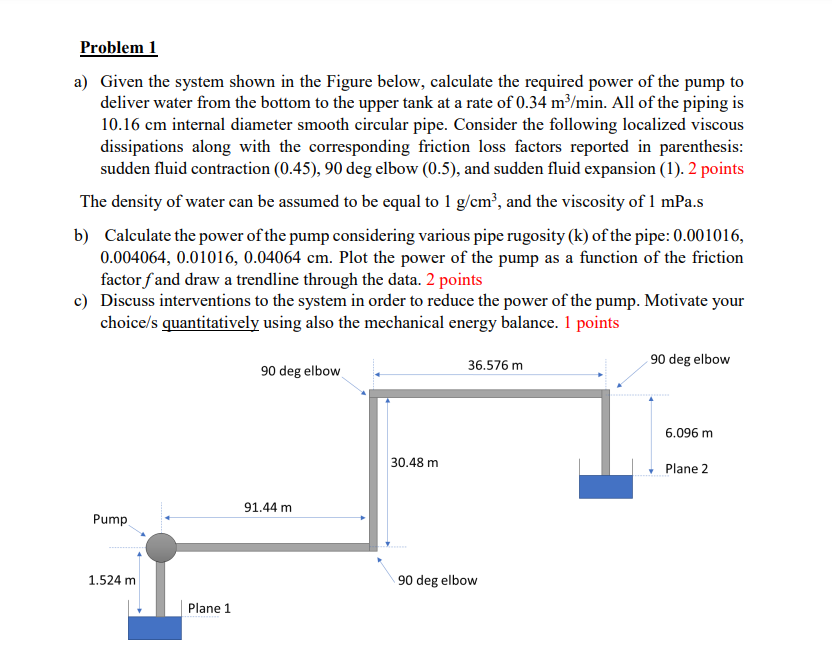
Question: Problem 1 a ) Given the system shown in the Figure below, calculate the required power of the pump to deliver water from the bottom
Problem
a Given the system shown in the Figure below, calculate the required power of the pump to
deliver water from the bottom to the upper tank at a rate of All of the piping is
internal diameter smooth circular pipe. Consider the following localized viscous
dissipations along with the corresponding friction loss factors reported in parenthesis:
sudden fluid contraction deg elbow and sudden fluid expansion points
The density of water can be assumed to be equal to and the viscosity of mPa.
b Calculate the power of the pump considering various pipe rugosity of the pipe:
Plot the power of the pump as a function of the friction
factor and draw a trendline through the data. points
c Discuss interventions to the system in order to reduce the power of the pump. Motivate your
choices quantitatively using also the mechanical energy balance. points Applying energy balance equation then,
For part a
For part b
The outlet temperature of the water for a heated section long:
The outlet temperature of the water for a heated section long:
Explanation:
Here, we derived the expression for temperature distribution with the help of energy balance equation in a control volume system that is
Step
For part c
So fully developed flow is constant and temperature varies linearly.
For developing flow decrease with increasing in distance. For part d
For uniform wall heating,
Explanation:
Here, we derived heat flux and and shows the mean fluid temperature for fully developed and developing flow conditions.
Answer
For part a
For part b
For part c The diagram is shown above.
For part d
Could you write a matlab code based the four questions and answers
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


