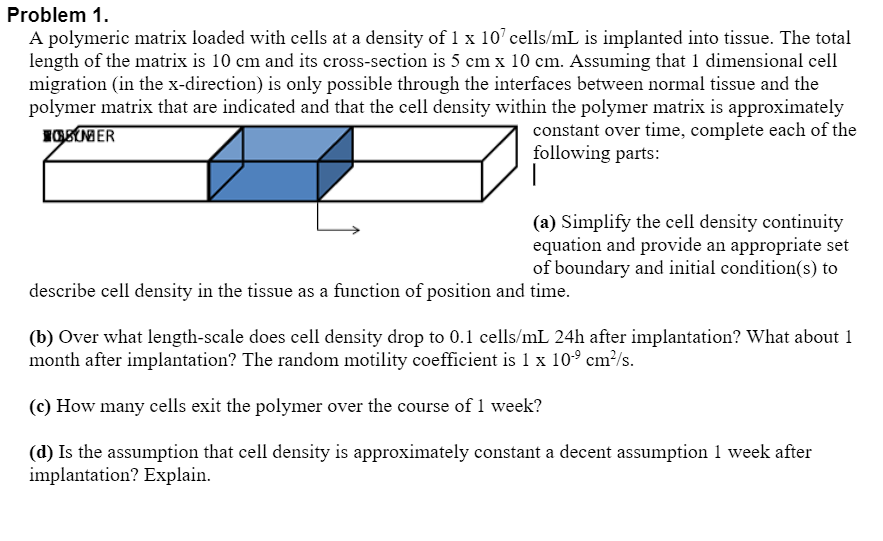
Problem 1. A polymeric matrix loaded with cells at a density of 1 x 10' cells/mL is implanted into tissue. The total length of the matrix is 10 cm and its cross-section is 5 cm x 10 cm. Assuming that 1 dimensional cell migration in the x-direction) is only possible through the interfaces between normal tissue and the polymer matrix that are indicated and that the cell density within the polymer matrix is approximately TOBUSNER constant over time, complete each of the following parts: (a) Simplify the cell density continuity equation and provide an appropriate set of boundary and initial condition(s) to describe cell density in the tissue as a function of position and time. (b) Over what length-scale does cell density drop to 0.1 cells/mL 24h after implantation? What about 1 month after implantation? The random motility coefficient is 1 x 10-9 cm-/s. (c) How many cells exit the polymer over the course of 1 week? (d) Is the assumption that cell density is approximately constant a decent assumption 1 week after implantation? Explain