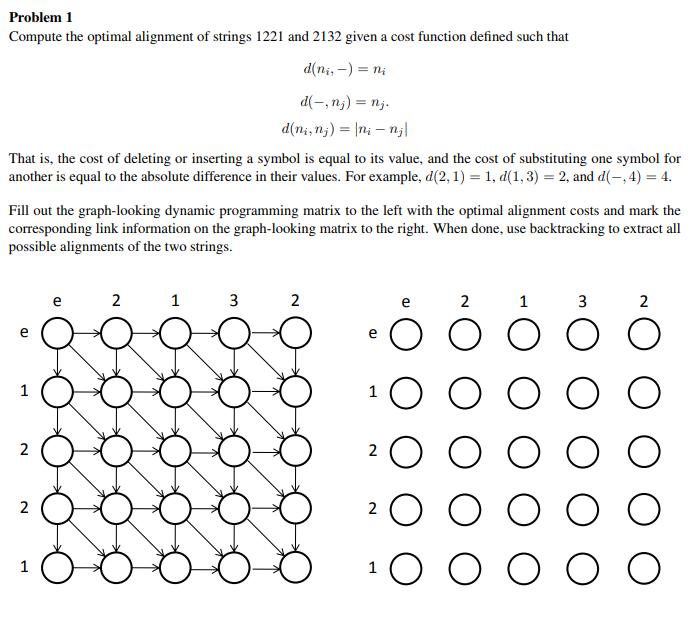
Problem 1 Compute the optimal alignment of strings 1221 and 2132 given a cost function defined such that d(ni,-)-n d(-, nj) = nj That is, the cost of deleting or inserting a symbol is equal to its value, and the cost of substituting one symbol for another is equal to the absolute difference in their values. For example, d(2, 1)-1, d(1,3)-2, and d(-,4)-4 Fill out the graph-looking dynamic programming matrix to the left with the optimal alignment costs and mark the corresponding link information on the graph-looking matrix to the right. When done, use backtracking to extract all possible alignments of the two strings