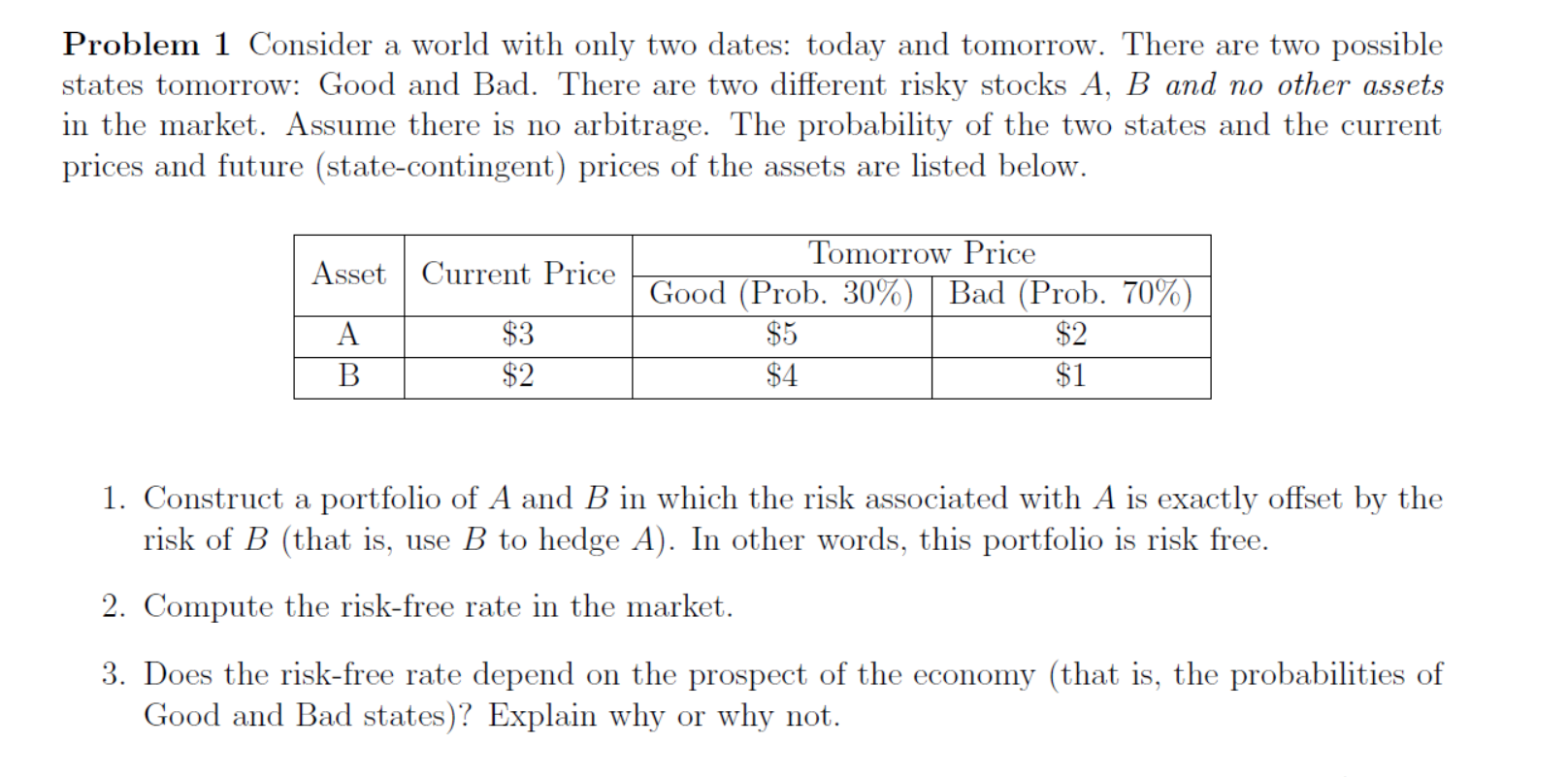
Problem 1 Consider a world with only two dates: today and tomorrow. There are two possible states tomorrow: Good and Bad. There are two different risky stocks A, B and no other assets in the market. Assume there is no arbitrage. The probability of the two states and the current prices and future (state-contingent) prices of the assets are listed below. Tomorrow Price | Asset | Current Price Good (Prob. 30%) | Bad (Prob. 70%) i A $3 B $2 $4 $1 $2 1. Construct a portfolio of A and B in which the risk associated with A is exactly offset by the risk of B (that is, use B to hedge A). In other words, this portfolio is risk free. 2. Compute the risk-free rate in the market. 3. Does the risk-free rate depend on the prospect of the economy (that is, the probabilities of Good and Bad states)? Explain why or why not. Problem 1 Consider a world with only two dates: today and tomorrow. There are two possible states tomorrow: Good and Bad. There are two different risky stocks A, B and no other assets in the market. Assume there is no arbitrage. The probability of the two states and the current prices and future (state-contingent) prices of the assets are listed below. Tomorrow Price | Asset | Current Price Good (Prob. 30%) | Bad (Prob. 70%) i A $3 B $2 $4 $1 $2 1. Construct a portfolio of A and B in which the risk associated with A is exactly offset by the risk of B (that is, use B to hedge A). In other words, this portfolio is risk free. 2. Compute the risk-free rate in the market. 3. Does the risk-free rate depend on the prospect of the economy (that is, the probabilities of Good and Bad states)? Explain why or why not