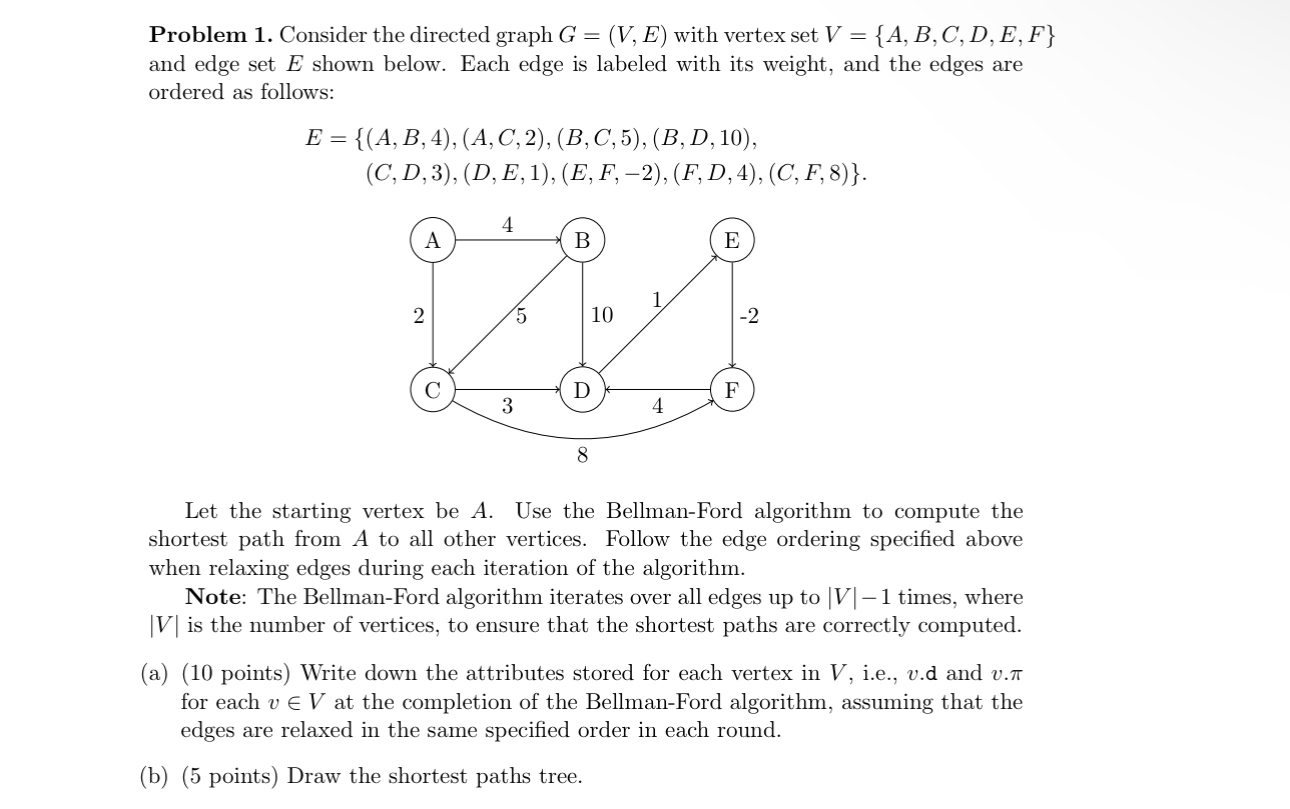
Problem $1.$ Consider the directed graph $G=(V,E)$ with vertex set $V=\{A,B,C,D,E,F\}$ and edge set $E$ shown below. Each edge is labeled with its weight, and the edges are ordered as follows:

$\}$

$\{(C,D,3),(D,E,1),(E,F,-2),(F,D,4),(C,F,8)$

Let the starting vertex be $A.$ Use the Bellman$-$Ford algorithm to compute the shortest path from $A$ to all other vertices. Follow the edge ordering specified above when relaxing edges during each iteration of the algorithm.

Note: The Bellman$-$Ford algorithm iterates over all edges up to $|V|-1$ times, where $|V|$ is the number of vertices, to ensure that the shortest paths are correctly computed.

$($a$)(10$ points$)$ Write down the attributes stored for each vertex in $V,$ i$.$e$.,v.$ d and $v.$ for each vinV at the completion of the Bellman$-$Ford algorithm, assuming that the edges are relaxed in the same specified order in each round.

$($b$)(5$ points$)$ Draw the shortest paths tree.