problem #1

Consider the linear transformation T : R3 R3 given by reflection about the plane P : x + 2y z = 0, that is, T(v) = v 2projnv, where n is any normal vector for P and v R3.

(a) Find the standard matrix A = [T] for T.

(b) If n is any normal vector to P, find T(n) and use the result to find aneigenvalue of A

(c) If v is any vector in the plane P, find T(v) using the fact that T isreflection about P. Use the result to find another eigenvalue of A

(d) Find eigenspaces corresponding to eigenvalues obtained in (b) and (c)using the fact that T is reflection about P (visualize the effect of the reflectionon vectors in (b) and (c)). Explain.

(e) Find the characteristic polynomial of A and eigenvalues of A

(f) Find a basis for each eigenspace of A. Show all step

Problem # 2

Consider the linear transformation T : R3 R3 defined by

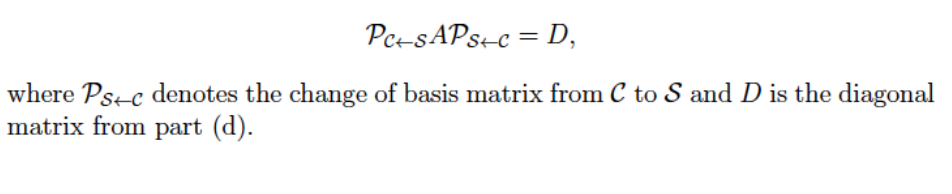
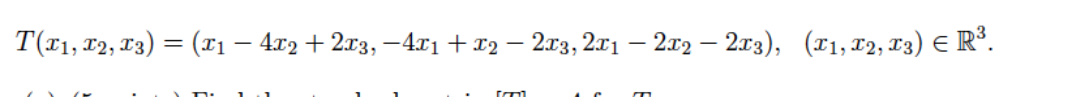
paesA'psw = D: where 73ch denotes the change of basis matrix from C to S and D is the diagonal matrix from part (d). \f