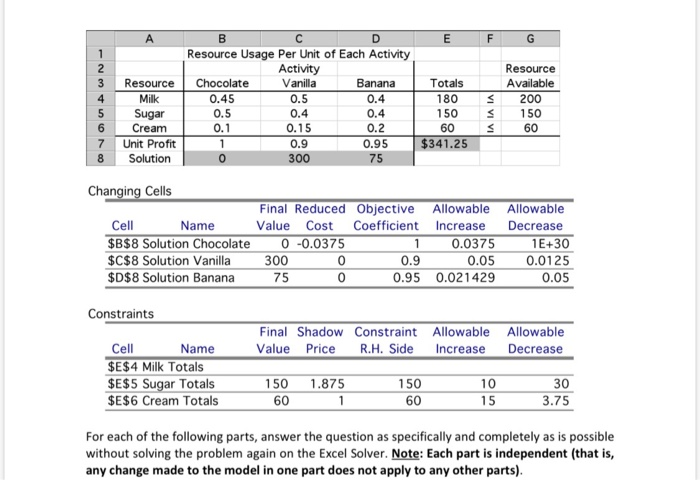
Question: Problem #1 - Ken and Larry, Inc., supplies its ice cream parlors with three flavors of ice cream: chocolate, vanilla, and banana. Due to extremely
Problem #1 - Ken and Larry, Inc., supplies its ice cream parlors with three flavors of ice cream: chocolate, vanilla, and banana. Due to extremely hot weather and a high demand for its products, the company has run short of its supply of ingredients: milk, sugar, and cream. Hence, they will not be able to fill all the orders received from their retail outlets, the ice cream parlors. Due to these circumstances, the company has decided to choose the amount of each flavor to produce that will maximize total profit, given the constraints on supply of the basic ingredients. The chocolate, vanilla, and banana flavors generate, respectively, $1.00, $0.90, and $0.95 of profit per gallon sold. The company has only 200 gallons of milk, 150 pounds of sugar, and 60 gallons of cream left in its inventory. The linear programming formulation for this problem is shown below in algebraic form. Let C = gallons of chocolate ice cream produced V=gallons of vanilla ice cream produced B = gallons of banana ice cream produced Maximize Profit = 1.00 C+0.90 V +0.95 B, subject to Milk: 0.45 C+0.50 +0.40 B 5 200 gallons Sugar: 0.50 C +0.40 V +0.40 B S 150 pounds Cream: 0.10 C +0.15 V +0.20 BS 60 gallons C20, V20, B 20. This problem was solved using the Excel Solver. The spreadsheet (already solved) and the sensitivity report are shown below. [Note: The numbers in the sensitivity report for the milk constraint are missing on purpose, since you will be asked to fill in these numbers in part (f).] E F G U AWN Resource Milk Sugar Cream Unit Profit Solution Resource Usage Per Unit of Each Activity Activity Chocolate Vanilla Banana 0.45 0.5 0.4 0.4 0.4 0.1 0.2 0.95 0 300 75 Totals 180 150 60 $341.25 Resource Available 200 150 60 S Changing Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $B$8 Solution Chocolate 0 -0.0375 1 0.03751E+30 $C$8 Solution Vanilla 300 0 0.9 0.05 0.0125 $D$8 Solution Banana 75 0 0.95 0.021429 0 .05 Constraints Final Shadow Constraint Allowable Value Price R.H. Side Increase Allowable Decrease Cell Name $E$4 Milk Totals $E$5 Sugar Totals $E$6 Cream Totals 1.875 150 60 150 60 10 15 30 3.75 For each of the following parts, answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver. Note: Each part is independent (that is, any change made to the model in one part does not apply to any other parts) (e) Suppose the company has the opportunity to buy an additional 15 pounds of sugar at a total cost of $15. Should they? Explain. (3 points) (f) Fill in all of the sensitivity report information for the milk constraint, given just the optimal solution for this problem. Explain how you were able to deduce each number. (3 points)