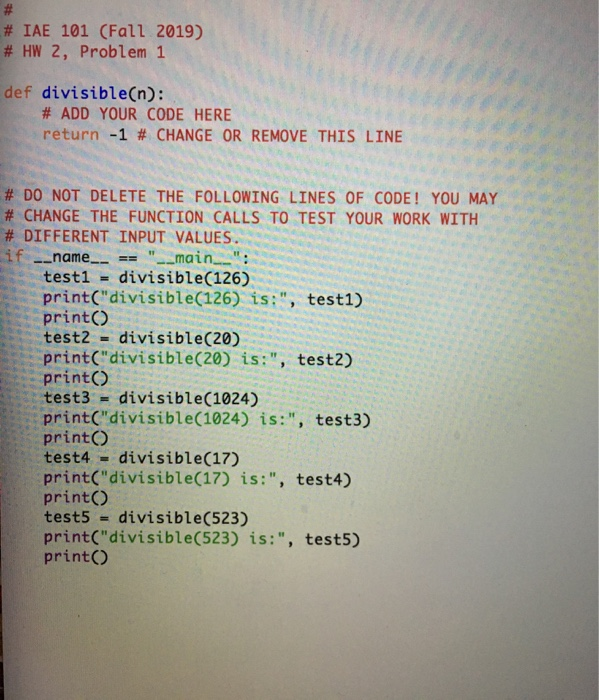
Problem 1: Testing for divisibility Suppose I want to know whether a number, x is evenly divisible by a number y. When I use the phrase "evenly divisible", I mean division without any remainder. So, x is evenly divisible by y if we can divide x by y without leaving any remainder behind (the remainder is equal to 0). Sometimes it is easy to tell whether one number evenly divides another just by looking. If y is 2, then we know that all even numbers (numbers ending with 0, 2, 4, 6, or 8) can be evenly divided by 2 and that all odd numbers (numbers ending with 1, 3, 5, 7, or 9) cannot be evenly divided by 2. The same is true if y is equal to 5. All numbers ending in 5 or 0 can be evenly divided by 5. However, there are many cases of divisibility that are harder to check. Determining whether a number is evenly divisible by 3 or 7 can be difficult to do just by looking, especially for larger numbers. Computer can always do this easily. Recall that the modulus operator, %, is used to return just the remainder from an integer division operation. The expression, x %y, which is read as x modulo y (or x mod y), integer divides x by y and returns just the remainder of the division operation. We can use this to easily determine whether x is evenly divided by y. Ifx % y evaluates to 0, then we can conclude that .x is evenly divisible by y. The file "hw2problem 1.py" contains a Python function called divisible (), which takes one argument, an integer n. Complete the body of the function to do the following: First, create an empty list. Then for each of the integers I through 9, determine whether it evenly divides n. If so, then add True to the list. If not, then add False to the list. Once you have checked whether n is divisible by each of the integers from 1 through 9, return the list of Booleans. For example, suppose the input n is equal to 126. 126 is evenly divisible by 1, 2, 3, 6, 7, and 9. So, I will add True at the first three elements, then two False entries for 4 and 5, then True for 6 and 7, False for 8, and True for 9. The result list can be seen in the table below. I then return the list.. Examples: Function Call divisible (126) divisible (20) divisible (1024) divisible (17) divisible (539 Return Value [True, True, True, False, False, True, True, False, Truel [True, True, False, True, True, False, False, False, False] [True, True, False, True, False, False, False, True, False] [True, False, False, False, False, False, False, False, False] [True, False, False, False, False, False, True, False, False] # #IAE 101 (Fall 2019) # HW 2, Problem 1 def divisible(n): # ADD YOUR CODE HERE return -1 # CHANGE OR REMOVE THIS LINE # DO NOT DELETE THE FOLLOWING LINES OF CODE! YOU MAY # CHANGE THE FUNCTION CALLS TO TEST YOUR WORK WITH # DIFFERENT INPUT VALUES. == "__main__": divisible(126) print("divisible(126) is:", test1) if -_name_ test1 print() test2 = divisible(20) print("divisible(20) is:", test2) print() test3 divisible (1024) print("divisible (1024) is:", test3) = print() test4 divisible(17) print("divisible(17) is:", test4) = print() test5 divisible(523) print("divisible (523) is:", test5) print()