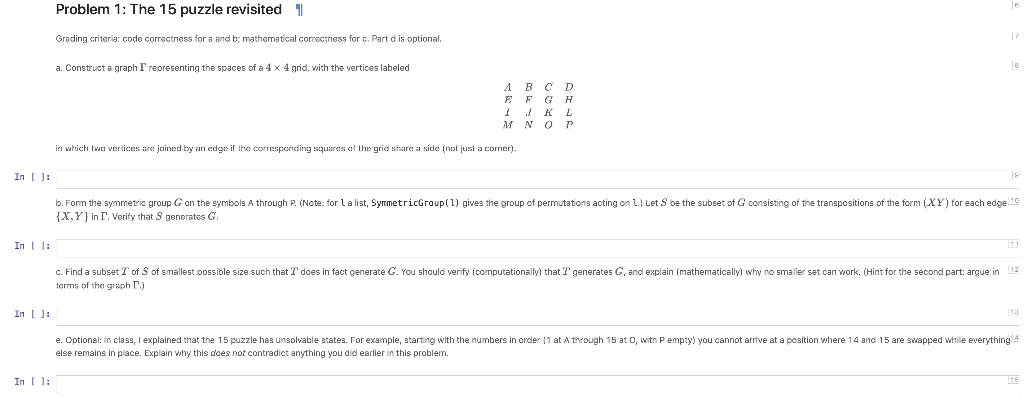
Problem 1: The 15 puzzle revisited 1 Grading criteria: code correctness for a and b; mathematical correctness for c. Part d is optional. a. Construct a graph I representing the spaces of a 4 x 4 grid, with the vertices labeled A E I M B F J N C G K O D H L P in which twa vertices are joined by an edge if the corresponding squares of the grid share a side (not just a correr). In ( ): b. For the symmetric group G on the symbols A through P. (Note: for L a list, SymmetricGroupil) gives the group of permutations acting on L. Let S be the subset of G consisting of the transpositions of the form (XY) for each edge 10 {X,Y} in T. Verify that generates G. In : 12 c. Find a subset T of S of smallest possible size such that I does in fact generate G. You should verify (computationally that I generates G, and explain (mathematically, why no smaller set can work. (Hint for the second part: argue in terms of the graph T.) In ) : e. Optional: in class. I explained that the 15 puzzle has unsolvable states. For example, starting with the numbers in order (1 at A through 15 at 0, with P empty) you cannot arrive at a position where 14 and 15 are swapped while everything 4 else remains in place. Explain why this does not contradict anything you did earlier in this problem. In 1: Problem 1: The 15 puzzle revisited 1 Grading criteria: code correctness for a and b; mathematical correctness for c. Part d is optional. a. Construct a graph I representing the spaces of a 4 x 4 grid, with the vertices labeled A E I M B F J N C G K O D H L P in which twa vertices are joined by an edge if the corresponding squares of the grid share a side (not just a correr). In ( ): b. For the symmetric group G on the symbols A through P. (Note: for L a list, SymmetricGroupil) gives the group of permutations acting on L. Let S be the subset of G consisting of the transpositions of the form (XY) for each edge 10 {X,Y} in T. Verify that generates G. In : 12 c. Find a subset T of S of smallest possible size such that I does in fact generate G. You should verify (computationally that I generates G, and explain (mathematically, why no smaller set can work. (Hint for the second part: argue in terms of the graph T.) In ) : e. Optional: in class. I explained that the 15 puzzle has unsolvable states. For example, starting with the numbers in order (1 at A through 15 at 0, with P empty) you cannot arrive at a position where 14 and 15 are swapped while everything 4 else remains in place. Explain why this does not contradict anything you did earlier in this problem. In 1