Problem $1$:

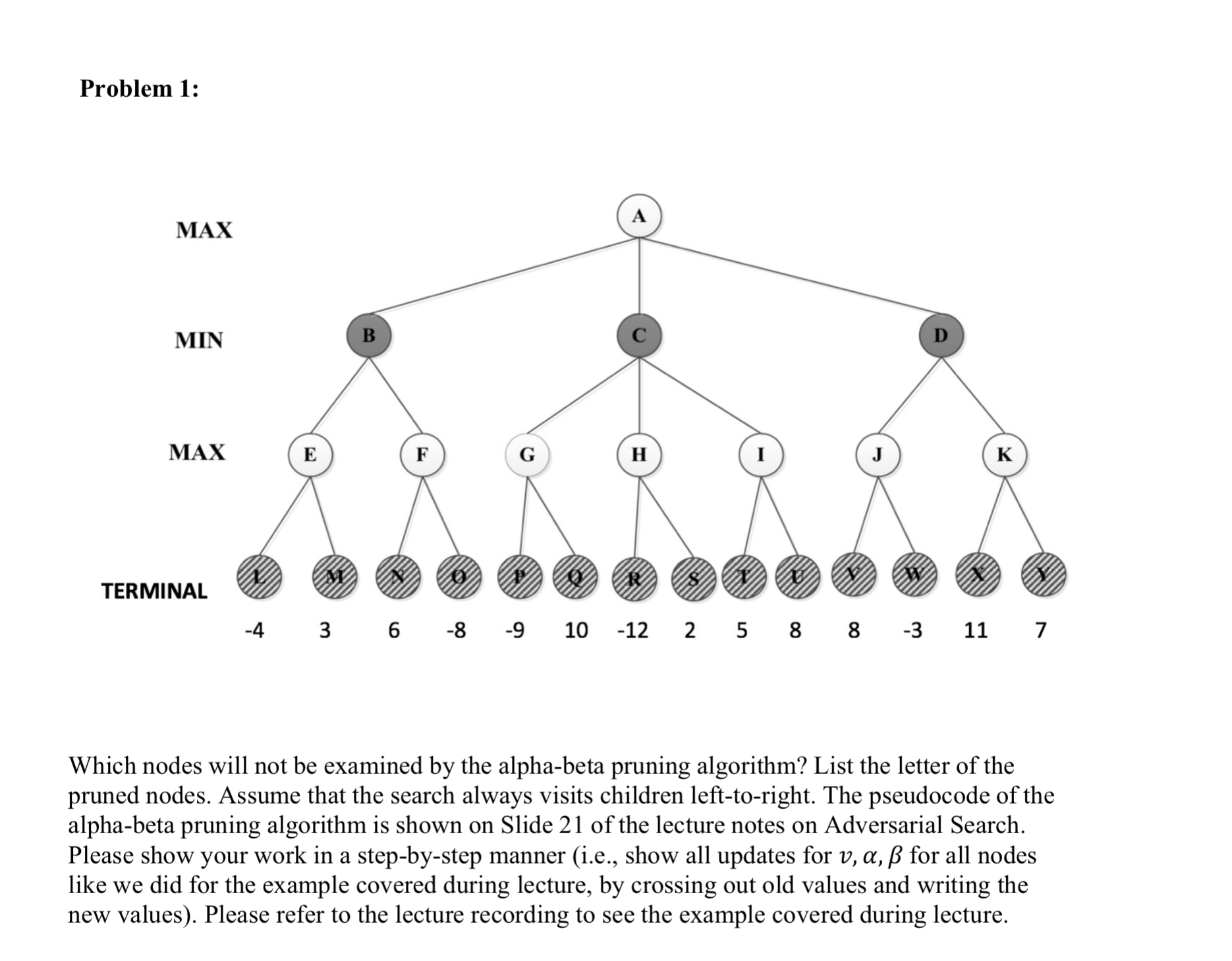
Which nodes will not be examined by the alpha$-$beta pruning algorithm? List the letter of the pruned nodes. Assume that the search always visits children left$-$to$-$right. The pseudocode of the alpha$-$beta pruning algorithm is shown on Slide $21$ of the lecture notes on Adversarial Search. Please show your work in a step$-$by$-$step manner $($i$.$e$.,$ show all updates for $\backslash ($ v$,\backslash$alpha$,\backslash$beta $\backslash )$ for all nodes like we did for the example covered during lecture, by crossing out old values and writing the new values$).$ Please refer to the lecture recording to see the example covered during lecture. Problem $2$:

You have the task of scheduling several courses. There is a total of $5$ courses, and there are $3$ professors who you will assign to teach the various courses. Each course will be taught by a single professor. A given professor can teach more than one course, as long as the courses do not overlap in terms of meeting time. The courses and professors are listed below.

The courses are as follows:

$-$ Course $1$ meeting time is $9$:$00-10$:$00$ am

$-$ Course $2$ meeting time is $9$:$30-10$:$30$ am

$-$ Course $3$ meeting time is $\backslash (10$: $15-11$: $15\backslash$mathrm$\{$am$\}\backslash )$

$-$ Course $4$ meeting time is $\backslash (10$: $15-11$: $15\backslash$mathrm$\{$am$\}\backslash )$

$-$ Course $5$ meeting time is $\backslash (10$: $45-11$: $45\backslash$mathrm$\{$am$\}\backslash )$

The professors are as follows:

$-$ Professor X$,$ who is available to teach Courses $1,2,3,4,5.$

$-$ Professor Y$,$ who is available to teach Courses $2,3,4,5.$

$-$ Professor Z$,$ who is available to teach Courses $3,4.$

$($a$)$ Formulate this as a constraint satisfaction problem. That is$,$ define the variables, the domains, and the constraints. Let the variables be the courses $($C$1-$ C$5).$ Do not enforce the unary and binary constraints yet $($this will be done in part $($c$)).$ That means that the domain for each variable should be the full domain $\backslash (\backslash \{$X$,$ Y$,$ Z$\backslash \}\backslash )$ in part$($a$).$ Please remember to use the set notation for the domains $($for example, C$1$: $\backslash \{,\backslash \}).$ And the constraints are typically expressed as inequalities $($ for example, $\backslash (\backslash$mathrm$\{$C$\}1!=\backslash$quad $\backslash )).$

$($b$)$ Draw the corresponding constraint graph. $($c$)$ Run node consistency $($that is$,$ enforce the unary constraints$)$ and arc consistency $($that is$,$ enforce the binary constraints$).$ When you enforce the constraints, the domains of the variables will be reduced. You need to list the reduced domains and remaining constraints in part$($c$).$ If you enforce a constraint and it is no longer needed $($in other words, it becomes redundant$),$ then it should not be included in the list of remaining constraints in part$($c$).$ When a unary constraint is enforced, it can definitely be removed. When a binary constraint is enforced, you may or may not be able to remove it $($depends on whether it is still needed$).$

$($d$)$ Give all possible solutions to this constraint satisfaction problem.