Question: Problem 1. Write the mathematical formulation to solve this problem and solve the problem. The goal is to satisfy customer demand at minimal cost. Consider
Problem 1. Write the mathematical formulation to solve this problem and solve the problem. The goal is to satisfy customer demand at minimal cost. Consider that the system produces two products in two plants, with two possible warehouse locations, and the three customers demand the two products. It must be decided whether one or two warehouses are needed. 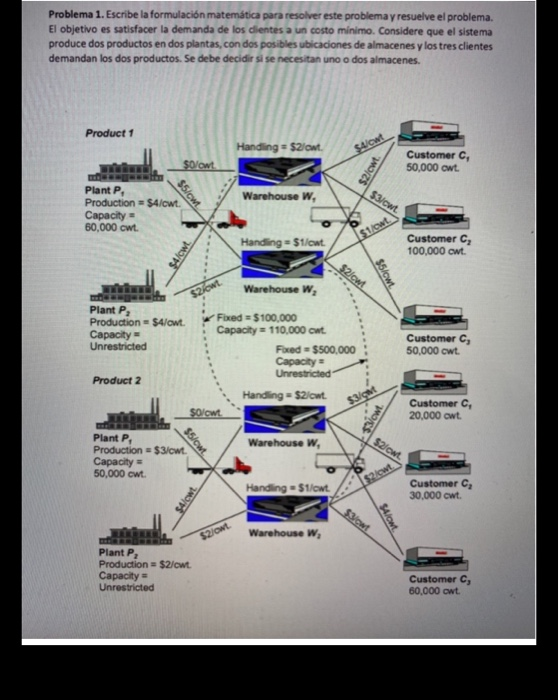

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


