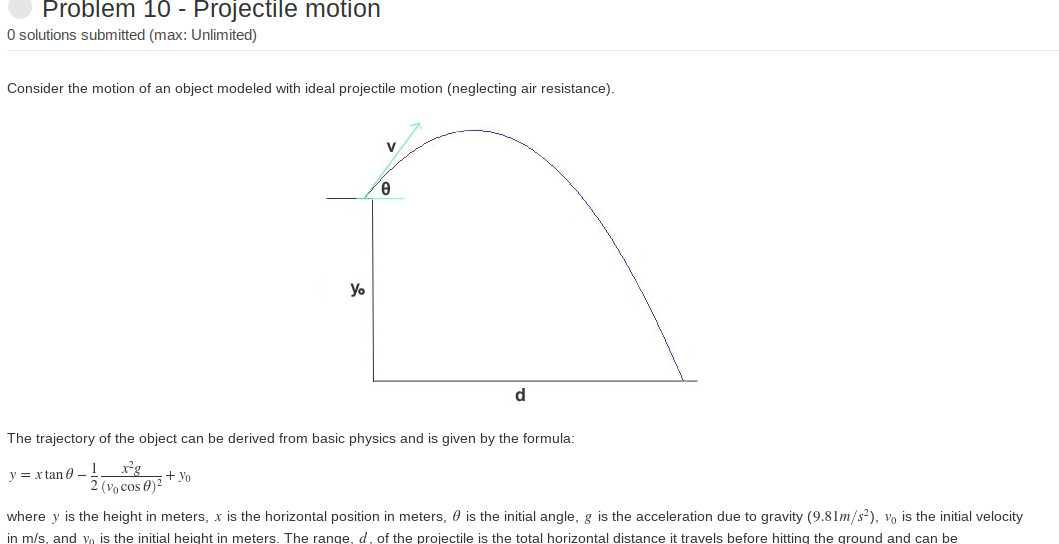
Problem 10 - Projectile motion O solutions submitted (max: Unlimited) Consider the motion of an object modeled with ideal projectile motion (neglecting air resistance). V yo d The trajectory of the object can be derived from basic physics and is given by the formula: xPg 2 (v, cos 02 y = x tan 0-1 + Yo where y is the height in meters, x is the horizontal position in meters, 6 is the initial angle, g is the acceleration due to gravity (9.81m/s2), V, is the initial velocity in m/s, and y, is the initial height in meters. The range, d, of the projectile is the total horizontal distance it travels before hitting the ground and can be Courses & Content LMS Integration Documentation & Support wnere y is the neight in meters, X is the norizontal position in meters, is the initial angie, g is the acceleration que to gravity (9.0m/s), Vo is the initial velocity in m/s, and yo is the initial height in meters. The range, d, of the projectile is the total horizontal distance it travels before hitting the ground and can be determined using the formula: d = Vocos (vo sin 0+ (v sin 0)2 + 2gyo) 8 Code has already been provided to define values for vo (units of meters/second), 0 (units of degrees), and yo (units of meters) and assigns them to the variables vo, theta, and yo, respectively. Add commands to compute the following and assign to the indicated output variables. Calculate d for the given inputs. This is a single scalar value. Assign this to the variable d. Create a row vector of 200 equally spaced x-values starting at 0 and ending at d and assign to the variable x. Create a row vector of 200 y-values that gives the height of the projectile corresponding to each x in the fist output and assign to the variable y Determine the coordinates (x, y) of the peak of the trajectory (i.e. the highest value of y and the corresponding value of x) and assign as a 2-element row vector to the variable xyPeak. You will need to use the max function in a different way to extract both the maximum value and the location in the vector (the index) where that maximum value occurs. Please see Matlab documentation on the max function. Solve this problem using only vectorized code with no loops or if statements. Points will be lost if you use these. Note the values of vo, theta, and yo are supplied to the function when it is run by MATLAB grader. Be sure not to overwrite these values in your code. ript C Reset I MATLAB Documentation 1 Vo = 20; % initial velocity in m/s 2 theta = 35; % initial angle in degrees 3 yo = 5; % initial height in meters