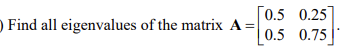
Problem 16. (7.2/27) a. Based on your answer to Problems 13 and 14, find closed formulas for the components 0.5 0.25 of the dynamical system x(t +1) = 0.5 0.75 x(t) , with initial value x, =e . Then do the same for the initial value x, = e, . Sketch the two trajectories. 0.5 0.25 b. Consider the matrix A = 0.5 0.75 Using technology, compute some powers of the matrix A, say, A , A', A ,.... What do you observe? Explain your answer carefully. a b c. If A = is an arbitrary regular transition matrix, what can you say about the powers A' as f goes to C d infinity?\fb Problem 14. (7.2/25) Consider a 2x2 matrices A of the form A = a d , where a, b, c, and d are positive numbers such that ate=b+d =1. (The matrix in Problem 13 has this form.) Such a matrix is called a regular transition matrix. Verify that and are eigenvectors of A. What are the associated eigenvalues? Is the absolute value of these eigenvalues more or less than 1? Sketch a phase portrait