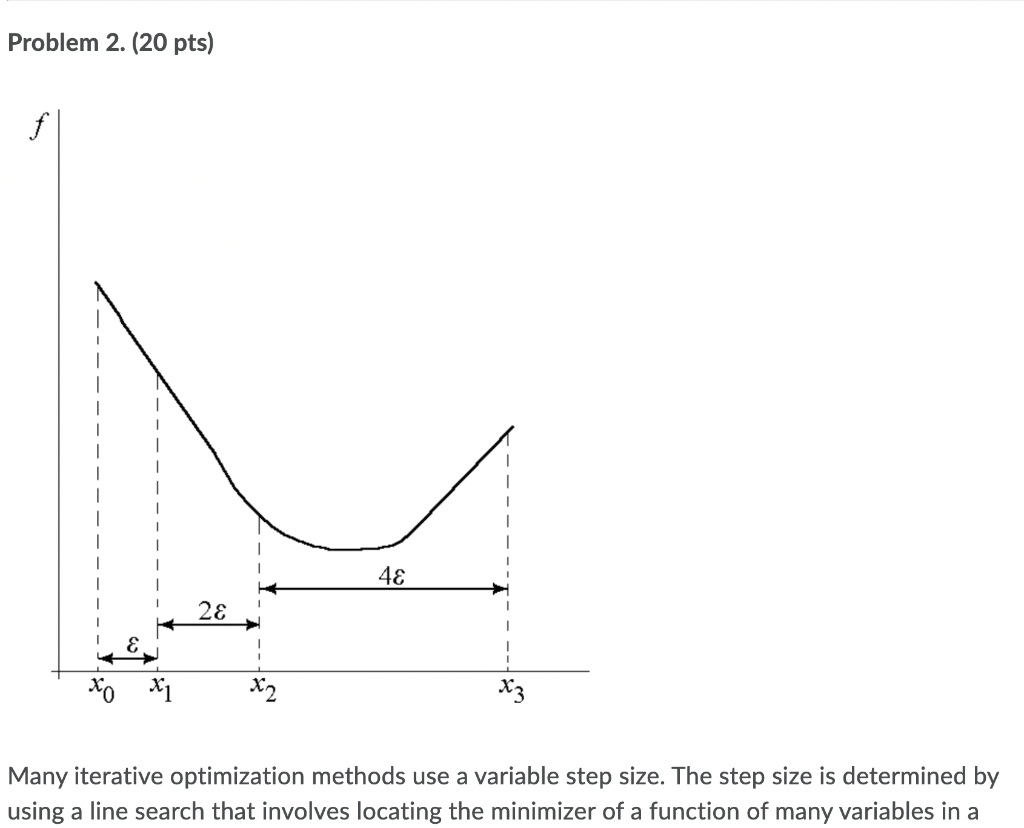
Problem 2. (20 pts) 4 2a E xo x1 X2 X3 Many iterative optimization methods use a variable step size. The step size is determined by using a line search that involves locating the minimizer of a function of many variables in a using a line search that involves locating the minimizer of a function of many variables in a specified direction d. This involves the location of an interval in which the minimizer lies and then the interval is reduced. Once the uncertainty interval is determined, one can use the Golden Section search or the Fibonacci method to reduce the uncertainty interval. We now describe a method that can be used to determine an interval containing the minimizer. We begin by evaluating the given function, sayf, at an initial point x(0). The next step is to evaluate the function at a second point which is a distance & from x(0), where & is the chosen parameter, that is, we evaluate f at x0) + d. We then continue to evaluate f at new points, successively doubling the distance between the points. The process stops when the function increases between two consecutive evaluations. In the one-dimensional example in the Figure, the function f increases between X2 and X3 and therefore the minimizer is bracketed in the interval [x1, x3] Consider now the function 2 1 10-11 : 12 f(x) = IxT X with the initial guess x) = [0.8 -0.25]" (0 = . Assume that the direction of travel is the negative gradient off. Take = 0.075. Bracket the minimizer, that is, use the above described method to find an initial uncertainty region. For more information on bracketing consult Subsection 7.7, page 123, of the textbook. Problem 2. (20 pts) 4 2a E xo x1 X2 X3 Many iterative optimization methods use a variable step size. The step size is determined by using a line search that involves locating the minimizer of a function of many variables in a using a line search that involves locating the minimizer of a function of many variables in a specified direction d. This involves the location of an interval in which the minimizer lies and then the interval is reduced. Once the uncertainty interval is determined, one can use the Golden Section search or the Fibonacci method to reduce the uncertainty interval. We now describe a method that can be used to determine an interval containing the minimizer. We begin by evaluating the given function, sayf, at an initial point x(0). The next step is to evaluate the function at a second point which is a distance & from x(0), where & is the chosen parameter, that is, we evaluate f at x0) + d. We then continue to evaluate f at new points, successively doubling the distance between the points. The process stops when the function increases between two consecutive evaluations. In the one-dimensional example in the Figure, the function f increases between X2 and X3 and therefore the minimizer is bracketed in the interval [x1, x3] Consider now the function 2 1 10-11 : 12 f(x) = IxT X with the initial guess x) = [0.8 -0.25]" (0 = . Assume that the direction of travel is the negative gradient off. Take = 0.075. Bracket the minimizer, that is, use the above described method to find an initial uncertainty region. For more information on bracketing consult Subsection 7.7, page 123, of the textbook