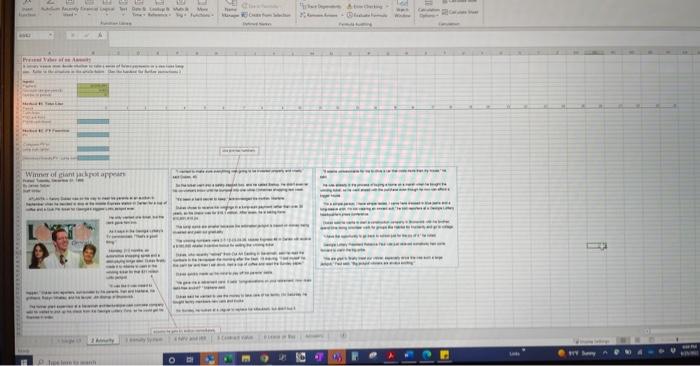
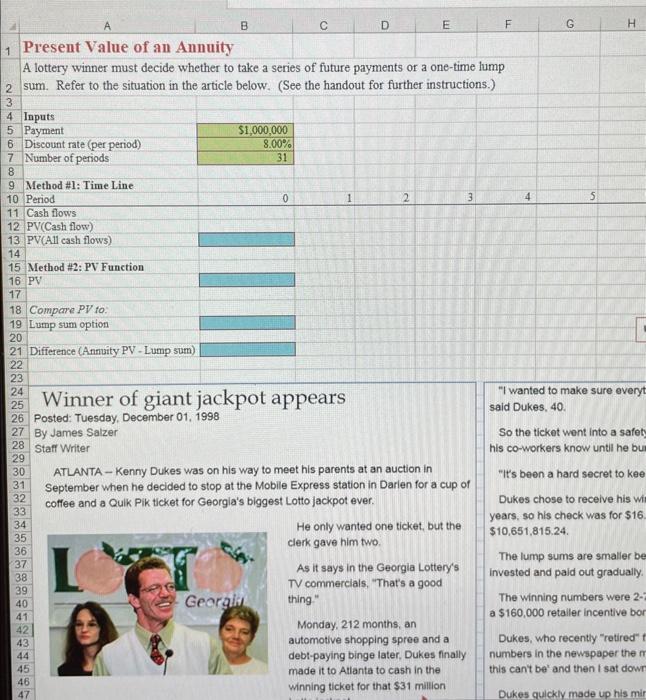
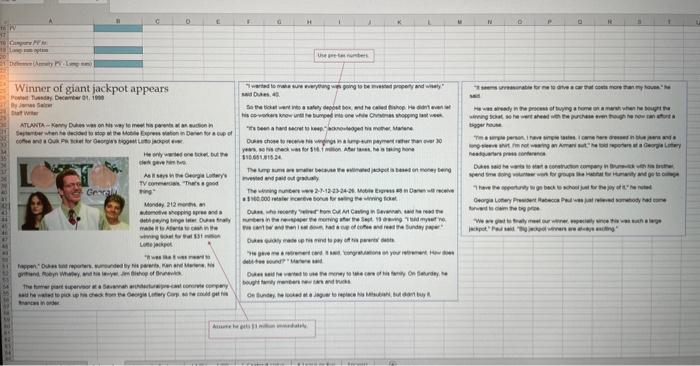
Problem #2 - Annuity This problem is based on article shown at the bottom of the spreadsheet. Initially assume an 8% discount rate. Enter the inputs in the green boxes, and then solve for the present value of an annuity in two ways. The first way is using a timeline. On the line that says "Cash Flows" enter the cash flow that will be received in each period. On the line below that, enter the PV of each cash flow. This is done with the same formula, PV=CF/(1+1)n. If you enter this formula correctly (lock in the discount rate using $ in front of that reference, i.e. $B6, and refer to the cell containing the period number for n ), then you only have to enter this formula once, in B12, and you can copy it all the way across to year 30 . Then just sum up this row of present values in B13 using the SUM function. This will give you the present value. The second way to calculate the present value is using the Excel PV function. Do this as described above in Problem #1. Q2. What is the present value of the annuity option assuming an 8% discount rate? Compare the present value of the annuity to the value of the lump sum. Enter the value of the (pretax) lump sum in B19 (see the article), and enter a formula for the difference in B21. Q3: At an 8% discount rate, is he better off taking the lump sum or the annuity? Q4: What is the present value of the annuity option assuming a 4% discount rate? Q5. At a 4% discount rate, is he better off taking the lump sum or the annuity? Now find the break-even discount rate, i.e., the rate at which the present values of both options are equal. You can do this using the Goal Seek tool under Data | What-if Analysis. Tell Goal Seek that you want to set the difference (cell B21) to zero by changing the discount rate (cell B6). Goal Seek will find the solution for you. Q6: At what discount rate is Kenny indifferent between the annuity and the lump sum? A lottery winner must decide whether to take a series of future payments or a one-time lump sum. Refer to the situation in the article below. (See the handout for further instructions.) 345InputsPaymet 5 Payment 7 Number of periods 9 Method #1: Time Line 10 Period 11 Cash flows 12 PV(Cash flow) 13. PV(All cash flows) 15 Method #2: PV Function 15 Method #2: PV Fu 16 PV 17 18 Compare PV fo: 19 Lump sum option 20 21 Difference (Annuity PV - Lump sum) 2221 27 Posted: Tuesday, \begin{tabular}{l|l|l} 30 & ATLANTA - Kenny Dukes was on his way to meet his parents at an auction in & "it's been a hard secret to kee \\ 31 & September when he decided to stop at the Mobile Express station in Darlen for a cup of \\ 32 & coffee and a Qulk Pik ticket for Georgla's biggest Lotto jackpot ever. & Dukes chose to receive his win \\ 33 & & He only wanted one ticket, but the \\ 34 & clerk gave him two. \\ $10,651,815.24. \end{tabular} Problem #2 - Annuity This problem is based on article shown at the bottom of the spreadsheet. Initially assume an 8% discount rate. Enter the inputs in the green boxes, and then solve for the present value of an annuity in two ways. The first way is using a timeline. On the line that says "Cash Flows" enter the cash flow that will be received in each period. On the line below that, enter the PV of each cash flow. This is done with the same formula, PV=CF/(1+1)n. If you enter this formula correctly (lock in the discount rate using $ in front of that reference, i.e. $B6, and refer to the cell containing the period number for n ), then you only have to enter this formula once, in B12, and you can copy it all the way across to year 30 . Then just sum up this row of present values in B13 using the SUM function. This will give you the present value. The second way to calculate the present value is using the Excel PV function. Do this as described above in Problem #1. Q2. What is the present value of the annuity option assuming an 8% discount rate? Compare the present value of the annuity to the value of the lump sum. Enter the value of the (pretax) lump sum in B19 (see the article), and enter a formula for the difference in B21. Q3: At an 8% discount rate, is he better off taking the lump sum or the annuity? Q4: What is the present value of the annuity option assuming a 4% discount rate? Q5. At a 4% discount rate, is he better off taking the lump sum or the annuity? Now find the break-even discount rate, i.e., the rate at which the present values of both options are equal. You can do this using the Goal Seek tool under Data | What-if Analysis. Tell Goal Seek that you want to set the difference (cell B21) to zero by changing the discount rate (cell B6). Goal Seek will find the solution for you. Q6: At what discount rate is Kenny indifferent between the annuity and the lump sum? A lottery winner must decide whether to take a series of future payments or a one-time lump sum. Refer to the situation in the article below. (See the handout for further instructions.) 345InputsPaymet 5 Payment 7 Number of periods 9 Method #1: Time Line 10 Period 11 Cash flows 12 PV(Cash flow) 13. PV(All cash flows) 15 Method #2: PV Function 15 Method #2: PV Fu 16 PV 17 18 Compare PV fo: 19 Lump sum option 20 21 Difference (Annuity PV - Lump sum) 2221 27 Posted: Tuesday, \begin{tabular}{l|l|l} 30 & ATLANTA - Kenny Dukes was on his way to meet his parents at an auction in & "it's been a hard secret to kee \\ 31 & September when he decided to stop at the Mobile Express station in Darlen for a cup of \\ 32 & coffee and a Qulk Pik ticket for Georgla's biggest Lotto jackpot ever. & Dukes chose to receive his win \\ 33 & & He only wanted one ticket, but the \\ 34 & clerk gave him two. \\ $10,651,815.24. \end{tabular}