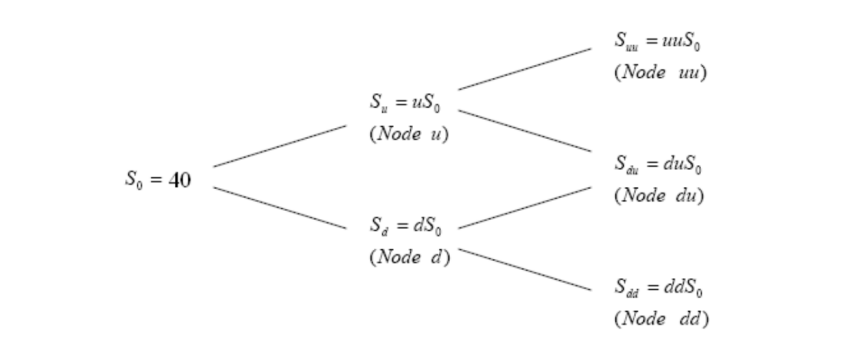
Problem 2. (Binomial model, 23') Consider a European call option with a maturity of 6 months and a strike of $41. The current spot stock price is $40. Consider a two-period binomial model. The stock has annual volatility of 30%, and the risk-free rate is 8% annualized and continuously compounded. The stock does not pay dividends. Suu=uuS0 Su=uS0 (Node uu) ( Node d) Sdd=ddS0 (Node dd) roblem 3. (Binomial model continued, 15') Consider the same stock as Problem 2. a. In Problem 2, we constructed a recombining binomial tree. For Problem 3, please construct a non-recombining binomial tree. (5') b. An Asian option is an exotic option, and its terminal payoffs are determined by the strike price K and the average stock price throughout the life of the option. Specifically, consider the following call option with terminal payoffs max{0,SK}, where S is the arithmetic average of the underlying stock prices at time 0 , at the end of 3 months, and at the end of 6 months for a price path. Let K=$40. What are the terminal payoffs of that option? Present them in your binomial tree in part (a). (5') c. Suppose you can only exercise the option at the end of 6 months and cannot exercise early. Price the option with your binomial tree. (5') (Hint: Asian options are path-dependent, so you should use a non-recombining binomial tree to price them. That is because, for path-dependent derivatives, nodes ud and du are different nodes with different paths, although they have the same stock price level). Problem 2. (Binomial model, 23') Consider a European call option with a maturity of 6 months and a strike of $41. The current spot stock price is $40. Consider a two-period binomial model. The stock has annual volatility of 30%, and the risk-free rate is 8% annualized and continuously compounded. The stock does not pay dividends. Suu=uuS0 Su=uS0 (Node uu) ( Node d) Sdd=ddS0 (Node dd) roblem 3. (Binomial model continued, 15') Consider the same stock as Problem 2. a. In Problem 2, we constructed a recombining binomial tree. For Problem 3, please construct a non-recombining binomial tree. (5') b. An Asian option is an exotic option, and its terminal payoffs are determined by the strike price K and the average stock price throughout the life of the option. Specifically, consider the following call option with terminal payoffs max{0,SK}, where S is the arithmetic average of the underlying stock prices at time 0 , at the end of 3 months, and at the end of 6 months for a price path. Let K=$40. What are the terminal payoffs of that option? Present them in your binomial tree in part (a). (5') c. Suppose you can only exercise the option at the end of 6 months and cannot exercise early. Price the option with your binomial tree. (5') (Hint: Asian options are path-dependent, so you should use a non-recombining binomial tree to price them. That is because, for path-dependent derivatives, nodes ud and du are different nodes with different paths, although they have the same stock price level)