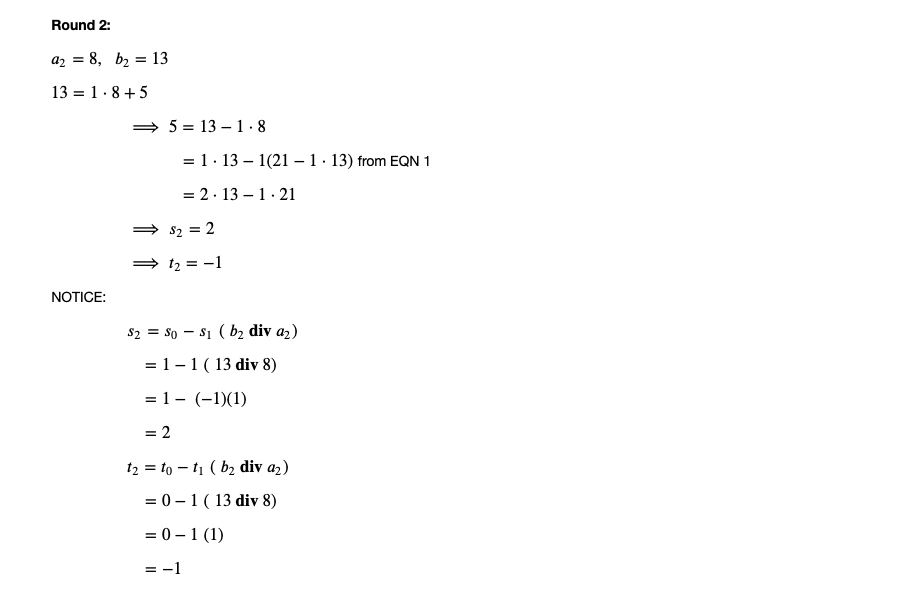
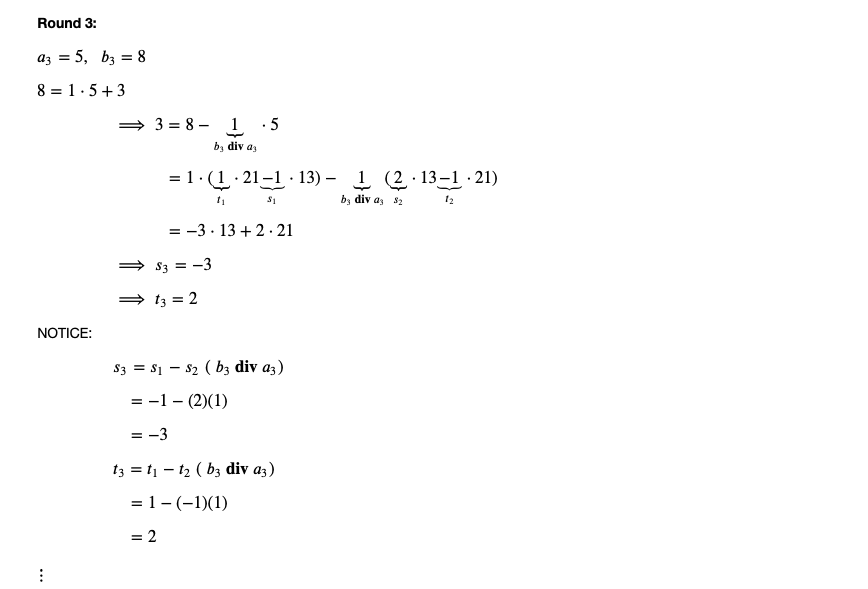
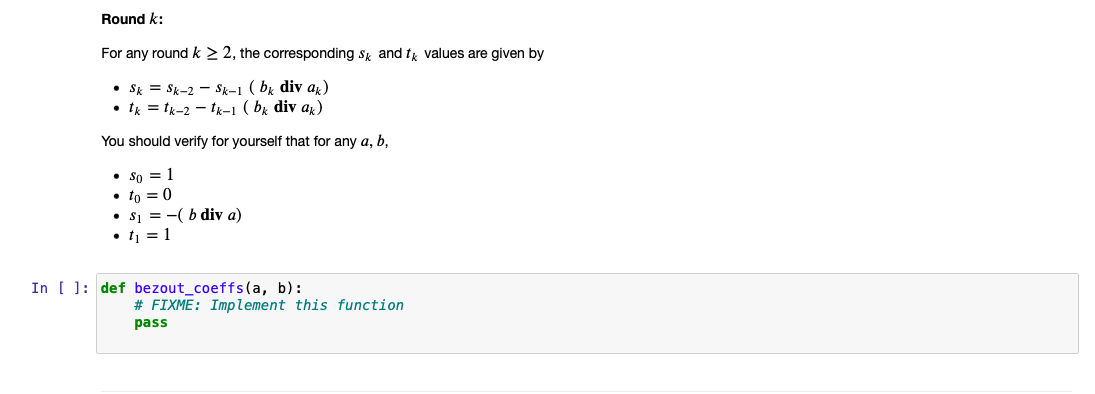
Problem 2: Create a function bezout_coeffs(a, b) that computes the Bezout coefficients s and t of a and b. 1. INPUT: a, b distinct integers 2. OUTPUT: {a: s, b: t} - dictionary where keys are the input integers and values are their corresponding Bezout coefficients. EXAMPLE: >> bezout_coeffs (414, 662) {414 : 8, 662 : -5} HINT: To come up with an algorithm for the function bezout_coeff(a,b) consider the following example: Suppose a = 13, b = 21. We seek s and t such that gcd(13,21) = 13s + 21t Let's begin by defining so = 1, to = 0, a = 13, bj = 21. At every round in attempting to attain the gcd, we will refer to s; and t; as the current coefficients of 13 and 21. Round 1: 21 = 1. 13 + 8 8= 21 -1.13 We will call this EQN 1 si = -(b, div a ) = -(21 div 13) = -1 t1 = 1 Round 2: a2 = 8, b2 = 13 13 = 1.8+5 = 5= 13-1.8 = = 1.13 - 1(21 - 1. 13) from EQN 1 = 2.13 - 1.21 =S2 = 2 t2 = -1 NOTICE: S2 = $o - $i (b2 div az) = 1-1 ( 13 div 8) = 1- (-1)(1) = 2 t2 = to - t (b2 div az) = 0 - 1 ( 13 div 8) = = 0 - 1 (1) = -1 Round 3: az = 5, b3 = 8 8 = 1.5+3 3 = 8 - b, divas 1.5 = = 1.1.21-1 13) - 1 (2.13-1 .21) b> div a3 82 Si 12 = -3.13 +2.21 = S3 = -3 atz = 2 NOTICE: S3 = $i - $2 (bz div az) = -1-(2)(1) = -3 t3 = t; - t2 (bz div az) = 1 -(-1)(1) = = 2 : Round k: For any round k > 2, the corresponding Sk and tk values are given by Sk = Sk-2 - Sk-1 (bx div ak) tk = tk-2-1-1 (bdiv ax) You should verify for yourself that for any a, b, so = 1 . to = 0 $i = -( b diva) . t = 1 In [ ]: def bezout_coeffs(a, b): # FIXME: Implement this function pass