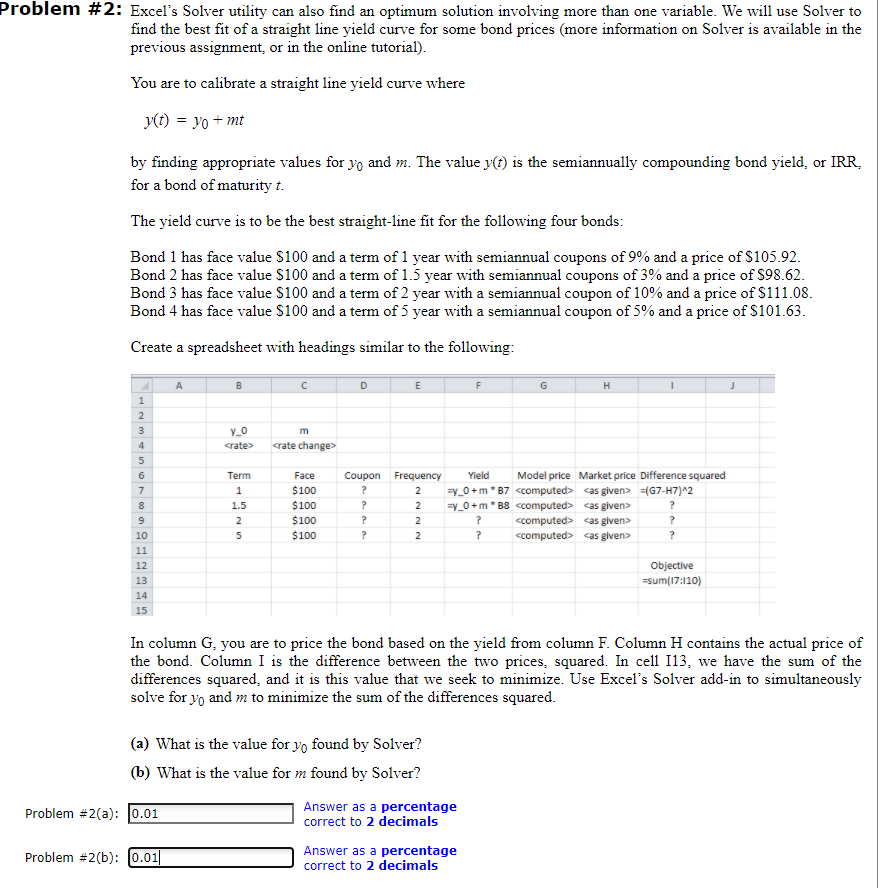
Problem #2: Excel's Solver utility can also find an optimum solution involving more than one variable. We will use Solver to find the best fit of a straight line yield curve for some bond prices (more information on Solver is available in the previous assignment or in the online tutorial). You are to calibrate a straight line yield curve where y(t) = yo + mt by finding appropriate values for yo and m. The value y(t) is the semiannually compounding bond yield. or IRR. for a bond of maturity t. The yield curve is to be the best straight-line fit for the following four bonds: Bond 1 has face value $100 and a term of 1 year with semiannual coupons of 9% and a price of $105.92. Bond 2 has face value $100 and a term of 1.5 year with semiannual coupons of 3% and a price of $98.62. Bond 3 has face value $100 and a term of 2 year with a semiannual coupon of 10% and a price of $111.08. Bond 4 has face value $100 and a term of 5 year with a semiannual coupon of 5% and a price of $101.63. Create a spreadsheet with headings similar to the following: H 1 2 3 m y_o crate> 4 crate changes 5 6 7 Term 1 1.5 2 5 Face $100 $100 $100 $100 Coupon Frequency ? ? ? ? NNNN Yield Model price Market price Difference squared =y_0+m* B7 ccomputed> =(G7-H7)^2 =v_0+ m * B8 ccomputed> 4 crate changes 5 6 7 Term 1 1.5 2 5 Face $100 $100 $100 $100 Coupon Frequency ? ? ? ? NNNN Yield Model price Market price Difference squared =y_0+m* B7 ccomputed> =(G7-H7)^2 =v_0+ m * B8 ccomputed>