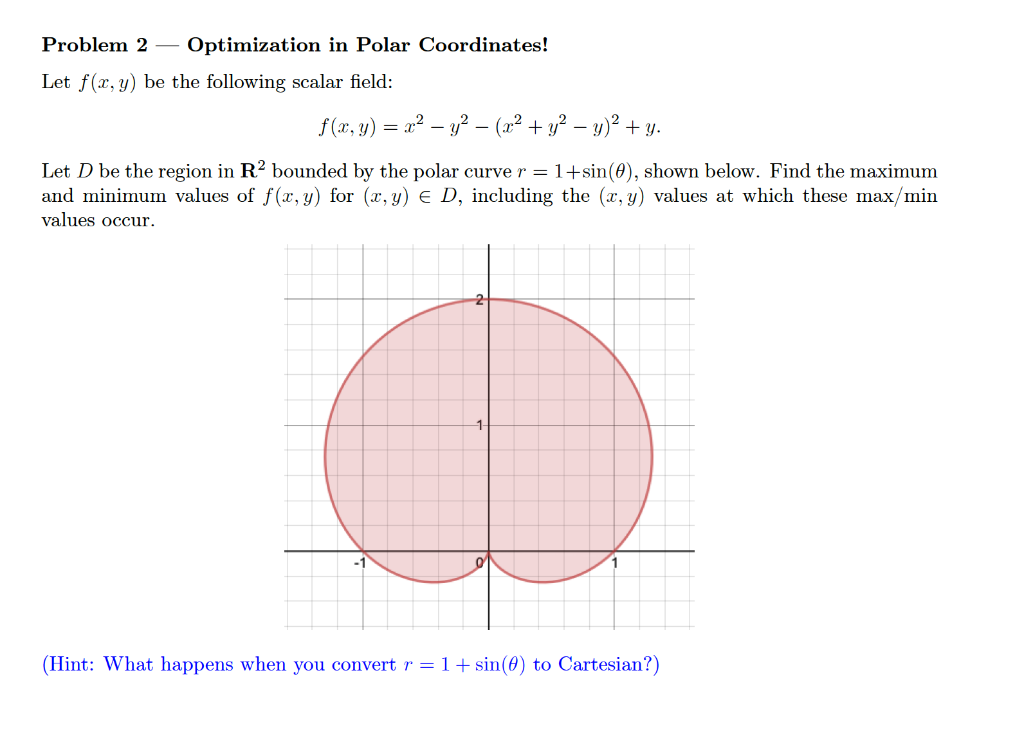
Problem 2 Optimization in Polar Coordinates! Let f(x,y) be the following scalar field: f(x,y) = x2 - y? (22 + y2 y)2 + y. Let D be the region in R bounded by the polar curve r = 1+sin(0), shown below. Find the maximum and minimum values of f(x,y) for (x,y) ED, including the (x, y) values at which these max/min values occur. 1 0 (Hint: What happens when you convert r = 1+ sin(() to Cartesian?) Problem 2 Optimization in Polar Coordinates! Let f(x,y) be the following scalar field: f(x,y) = x2 - y? (22 + y2 y)2 + y. Let D be the region in R bounded by the polar curve r = 1+sin(0), shown below. Find the maximum and minimum values of f(x,y) for (x,y) ED, including the (x, y) values at which these max/min values occur. 1 0 (Hint: What happens when you convert r = 1+ sin(() to Cartesian?)