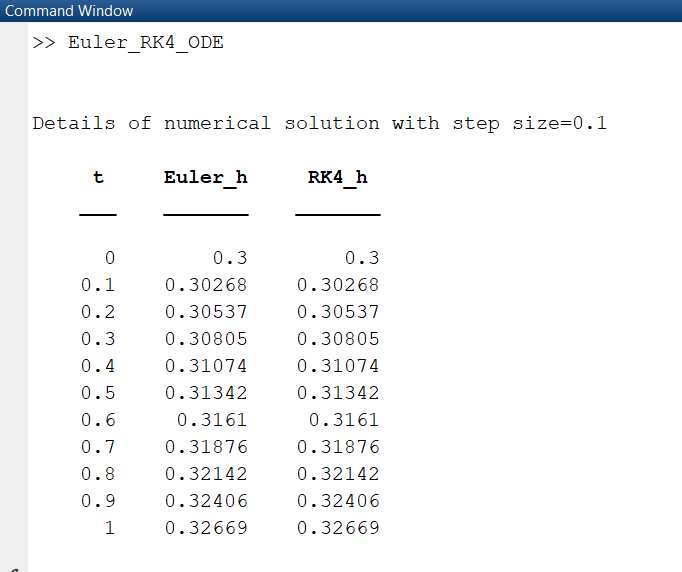
Problem 2 / Recitation The temporal evolution of the height of water & in a cylindrical tank of radius = 1m with periodic inflow and an outlet pipe can be determined by solving the following ODE (see for example class notes), @ = f(t) _ pAPiPE V 29h 2) dt PAtank: ' where f(t) = c[2 + sin (wt + cos(2wt))] , 3) c = 90kg/s, w = %Hz, p = 1000kg/m3, g = 9.81m/52, t is time, and A;qni and Ay, are the cross-sectional areas of the tank and the outlet pipe. Note that the cosine in f() is inside the sine and both are in radians. The outlet pipe has a radius of rpipe = 0.15m. At the initial time of = Os, the height of water in the tank is A (t = 0s) = 0.3m. For a step size of At = 1s, determine by hand the height of water in the tank at = 1s using the a) Explicit Euler method b) RK-2 modified Euler method c) Classical RK-4 method We have , C= 90 9- 9.81 40 = 2K . 32 Apipe = 7 x 60:15 ) P = 1000 Atonk = * * (1) - t. =D , h( 0 ) = 0 .3. 6% f ( + ) = c ( 2 + min ( c+ + con ( 2 wt ) ) ) dh - J ( t ) - PA pipe lagh = H (t, h ) f Alok forward Enler method ! h ( 1 ) = h (o) + 1 x H ( to, h(0) ) = 0 3 + 1 x 1 (0, 0. 3) = 013 268 1 m. calculations one done in MATLAB RK- 4 K = H ( 0 , 0 , 3 ) = 0 02 68 KZ = H ( 0 5 , 0 1 3 + 0 5 x k ) = 010268 ks = H ( 0. 5 , 0 . 3 + 0 5 x K ) = 010 2 68 ky = H ( 1, 0.3 + K3 ) = 0:026 1 h ( 1) = h/0) + % (ki+ 2k+ 2kq+ ky) = 0 32681 m.Command Window >> Euler RK4 ODE Details of numerical solution with step size=0. 1 t Euler h RK4 h 0 0.3 0.3 0 .1 0. 30268 0 . 30268 0.2 0. 30537 0. 30537 0.3 0. 30805 0 . 30805 0 . 4 0 . 31074 0 . 31074 0 . 5 0. 31342 0 . 31342 0 . 6 0. 3161 0. 3161 0.7 0. 31876 0 . 31876 0 . 8 0 . 32142 0 . 32142 0. 9 0. 32406 0 . 32406 1 0. 32669 0. 32669