Question: Problem 3 ( 4 0 points ) : Consider the 2 - DOF system shown in Figure 3 and answer the following questions: 1 -
Problem points:
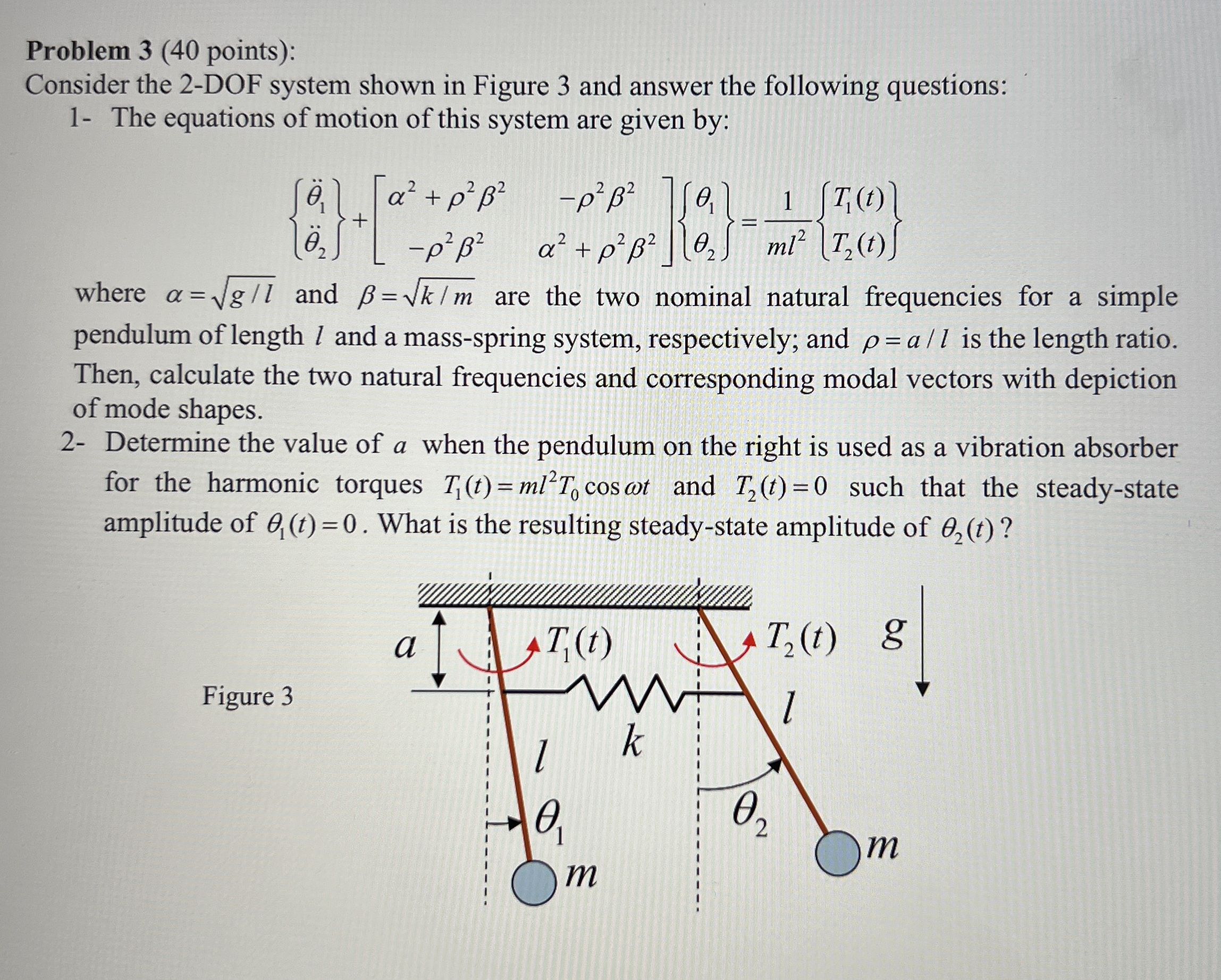
Consider the DOF system shown in Figure and answer the following questions:
The equations of motion of this system are given by:
where and are the two nominal natural frequencies for a simple pendulum of length and a massspring system, respectively; and is the length ratio. Then, calculate the two natural frequencies and corresponding modal vectors with depiction of mode shapes.
Determine the value of a when the pendulum on the right is used as a vibration absorber for the harmonic torques and such that the steadystate amplitude of What is the resulting steadystate amplitude of
Figure
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


