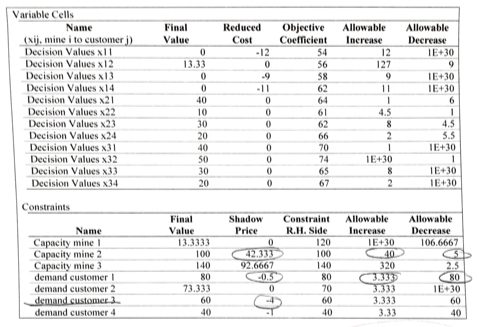
Problem 3 Consider the Blending Problem from class. A sensitivity report was calculated for the LP described on this page. Use the sensitivity report on the following page (some rows were purposely left of to answer parts a-d. Coalco produces coal at three mines and ships it to four customers. The cost per ton of producing coal and the ash and sulfur contient per ton of the coal for each mine are shown in Table 1. The number of tons of coal demanded by cach customer, the mine capacity, and the cost of shipping a ton of coal from mine i to each customer jare given in Table 2. It is required that the total amount of coal shipped to cach customer contain at most 5% ash and almost 4% sulfur. The objective is to minimize total cost Table 1: Mine Data Table 2: Demand (D). Capacity (C), and Production Ash Content Sulfur Content Shipping Costs (5) Mine Cost (P) (ash) sulfur) Shipping cost to 50 0.08 0.05 Customer Mias CA 55 0.06 0.04 3 62 0.04 0.03 100 120 1.40 Demand The condensed LP formulation is: Xy tons of coal from mine i to customer j; i = 1,2,3 and j = 1,2,3,4 min C 2*--*y) + -12-15 E yash-0.05 *y S 0:1 = 1,2,3,4 y sulfur -0.04 .*y S 0; j = 1,2,3,4 2). i = 1,2,3 y 20, 1 = 1,2,3,4 capacity constraint demand construit E Xy 20 for all ij The optimal solution is given in the table below. The total cost for this solution is $16.887. Solution Customer Final Value Reduced Cost Objective Coelicient Allowable increase Allowable Decrease IE+30 58 IE 30 IE30 Variable Cells Name (Nij, mine i to customer ;) Decision Values xil Decision Values x12 Decision Values x 13 Decision ValuesX14 Decision Values 21 Decision Values X22 Decision Values x23 Decision Values x 24 Decision Values X31 Decision Values x32 Decision Values x 33 Decision Values X34 4.5 5.5 IE+30 1E+30 1E+30 Constraints Shadow Price Final Value 13.3333 100 Constraint RH Side 120 100 Allowable Increase TE+30 40 Allowable Decrease 106.6667 42.333 026667 140 140 320 Name Capacity mine! Capacity mine 2 Capacity mine 3 demand customer demand customer 2 demand customers demand customer 4 NO 2.5 NO 1.30 73.333 33 3.333 40 Which decision variables (x) are basic and non-basic in this solution? Explain your reasoning Suppose shipping costs change so shipping from Mine 2 to Custome is now ss. Considering this updated shipping cost with the production cost of mine 2 (555) does the given solution still hold? If so, what is the decrease in the objective value (total costy? Explain your resoning, c. Coalco is happy with the current solution but wants to anticipate changes in customer demand. What can you tell Coalco about Customer 3's demand fluctuations? When would this solution not hold? His Shadow crise laineel l a .! Problem 3 Consider the Blending Problem from class. A sensitivity report was calculated for the LP described on this page. Use the sensitivity report on the following page (some rows were purposely left of to answer parts a-d. Coalco produces coal at three mines and ships it to four customers. The cost per ton of producing coal and the ash and sulfur contient per ton of the coal for each mine are shown in Table 1. The number of tons of coal demanded by cach customer, the mine capacity, and the cost of shipping a ton of coal from mine i to each customer jare given in Table 2. It is required that the total amount of coal shipped to cach customer contain at most 5% ash and almost 4% sulfur. The objective is to minimize total cost Table 1: Mine Data Table 2: Demand (D). Capacity (C), and Production Ash Content Sulfur Content Shipping Costs (5) Mine Cost (P) (ash) sulfur) Shipping cost to 50 0.08 0.05 Customer Mias CA 55 0.06 0.04 3 62 0.04 0.03 100 120 1.40 Demand The condensed LP formulation is: Xy tons of coal from mine i to customer j; i = 1,2,3 and j = 1,2,3,4 min C 2*--*y) + -12-15 E yash-0.05 *y S 0:1 = 1,2,3,4 y sulfur -0.04 .*y S 0; j = 1,2,3,4 2). i = 1,2,3 y 20, 1 = 1,2,3,4 capacity constraint demand construit E Xy 20 for all ij The optimal solution is given in the table below. The total cost for this solution is $16.887. Solution Customer Final Value Reduced Cost Objective Coelicient Allowable increase Allowable Decrease IE+30 58 IE 30 IE30 Variable Cells Name (Nij, mine i to customer ;) Decision Values xil Decision Values x12 Decision Values x 13 Decision ValuesX14 Decision Values 21 Decision Values X22 Decision Values x23 Decision Values x 24 Decision Values X31 Decision Values x32 Decision Values x 33 Decision Values X34 4.5 5.5 IE+30 1E+30 1E+30 Constraints Shadow Price Final Value 13.3333 100 Constraint RH Side 120 100 Allowable Increase TE+30 40 Allowable Decrease 106.6667 42.333 026667 140 140 320 Name Capacity mine! Capacity mine 2 Capacity mine 3 demand customer demand customer 2 demand customers demand customer 4 NO 2.5 NO 1.30 73.333 33 3.333 40 Which decision variables (x) are basic and non-basic in this solution? Explain your reasoning Suppose shipping costs change so shipping from Mine 2 to Custome is now ss. Considering this updated shipping cost with the production cost of mine 2 (555) does the given solution still hold? If so, what is the decrease in the objective value (total costy? Explain your resoning, c. Coalco is happy with the current solution but wants to anticipate changes in customer demand. What can you tell Coalco about Customer 3's demand fluctuations? When would this solution not hold? His Shadow crise laineel l a