Question: Let f : ID C be a nowhere-vanishing holomorphic function. For any positive integer m > 2, show that there exists a holomorphic function

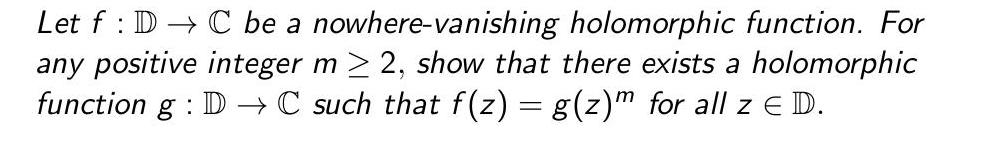
Let f : ID C be a nowhere-vanishing holomorphic function. For any

Let f : ID C be a nowhere-vanishing holomorphic function. For any positive integer m > 2, show that there exists a holomorphic function g : ID C such that f(z) = g(z) for all z E D.

Step by Step Solution

★★★★★

3.40 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

I Holomosphie st 2 FD4c be nowhere vanshing Holomoxphic function we Rnow that DCC be an be open ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

For any positive integer n determine (a) (b) i!(n - i)!

For any positive integer n, the MATLAB command P = pascal(n) will generate an n Ã n matrix P whose entries are given by The name pascal refers to Pascal's triangle, a triangular array of...

For any positive integer x, let xR be the integer whose binary representation is the reverse of the binary representation of x. (Assume no leading 0s in the binary representation of x.) Define the...

Let Y be an exponential random variable, where f Y (y) = e y, 0 y. For any positive integer n, show that P(n Y n + 1) = e n (1 e ). If p = 1 e , the "discrete" version of the exponential pdf...

Let Q be an n n orthogonal matrix. Use mathematical induction to prove each of the following. (a) (Qm)-l = (QT)m = (Qm)T for any positive integer m. (b) ||Qmx|| = ||x|| for any x Rm.

The geometric distribution can be used to model the number of trials before a certain event occurs. For example, we might flip a coin repeatedly until the first head appears. If the coin is fair, the...

If P is a linear program, let P denote the dual of P, and let Pk denote k application of the dual function. For example P 2 = (P ) is the dual of the dual of P. Show that for any positive integer...

In Problems 29 42, use the Binomial Theorem to find the indicated coefficient or term. The coefficient of x 2 in the expansion of THEOREM Binomial Theorem Let x and a be real numbers. For any...

In Problems 29 42, use the Binomial Theorem to find the indicated coefficient or term. The coefficient of x 4 in the expansion of THEOREM Binomial Theorem Let x and a be real numbers. For any...

In Problems 29 42, use the Binomial Theorem to find the indicated coefficient or term. The coefficient of x0 in the expansion of THEOREM Binomial Theorem Let x and a be real numbers. For any...

Question 3 2 pts Jaime agrees to buy a collector baseball signed by Babe Ruth (a famous player who played from 1914 to 1935) for $10,000 after Suzanna, the seller, provides a "certificate of...

I am responsible for paying all the bills at my company. I notice that we, the buyers, have received a shipment for which the bill of lading says, "freight prepaid". Am I correct that we will be...

Situation Roles: You = Account Manager at Amazon Para = Marketing Director at Blue Intelligence, Inc. Taylor = Your manager at Amazon Background: In addition to concerns over higher costs during your...

How can job costs be misrepresented? a.) Recording cost information for cost control. b.) Stating the level of completion to show performance. c.) Charging costs to the wrong jobs. d.) Assigning...

What are the major considerations for initiating a logistics alliance? In implementation? In maintenance?

Edward Lee manufactures and sells homemade wine, and he wants to develop a standard cost per litre. The following are required for production of a 250-litre batch: 120.00 litres of grape concentrate...

Required: 2a. Which Salesperson has the highest average revenue per sales order during the 12-month period? What was the amount? 2b. Which Salesperson has the lowest average revenue per sales order...

Read Case Study Google: Dont Be Evil Unless and answer the following: Given its mission of providing information to the world, should Google censor searches in China?

Prove the statement in Prob. 29 for general k = 1, 2, .

Compute f(6.5) from by cubic interpolation, using(10) f(6.0) = 0.1506 f(7.0) = 0.3001 f(7.5) = 0.2663 f(7.7) = 0.2346

Map the upper half z-plane onto the unit disk |w|

The venom of a black widow spider acts as a(n) __________ by mimicking the effects of acetylcholine. a. agonist b. protagonist c. antagonist d. glial cell

Which one of the following is NOT a function of glial cells? a. getting nutrients to the neurons b. generating action potentials c. cleaning up the remains of dead neurons d. generating myelin

Compare and contrast neuroimaging techniques for mapping the brains structure and function.