Problem $3.$ Minimum Cost. Path in a Grid $(30$ points total$)$

You are given a grid of size $mn$ where each cell $(i,j)$ has a non$-$negative cost

$C[i][j]$ associated with it$.$ Your task is to find the minimum cost path from the top$-$left

corner of the grid $(1,1)$ to the bottom$-$right corner $(m,n).$ You may only move either

right or down at any point in time.

Example:

$C=\left[\begin{array}{cccc}4& 5& 2& 8\\ 3& 4& 1& 1\\ 9& 2& 5& 7\\ 2& 1& 6& 4\\ 3& 4& 4& 2\end{array}\right]$

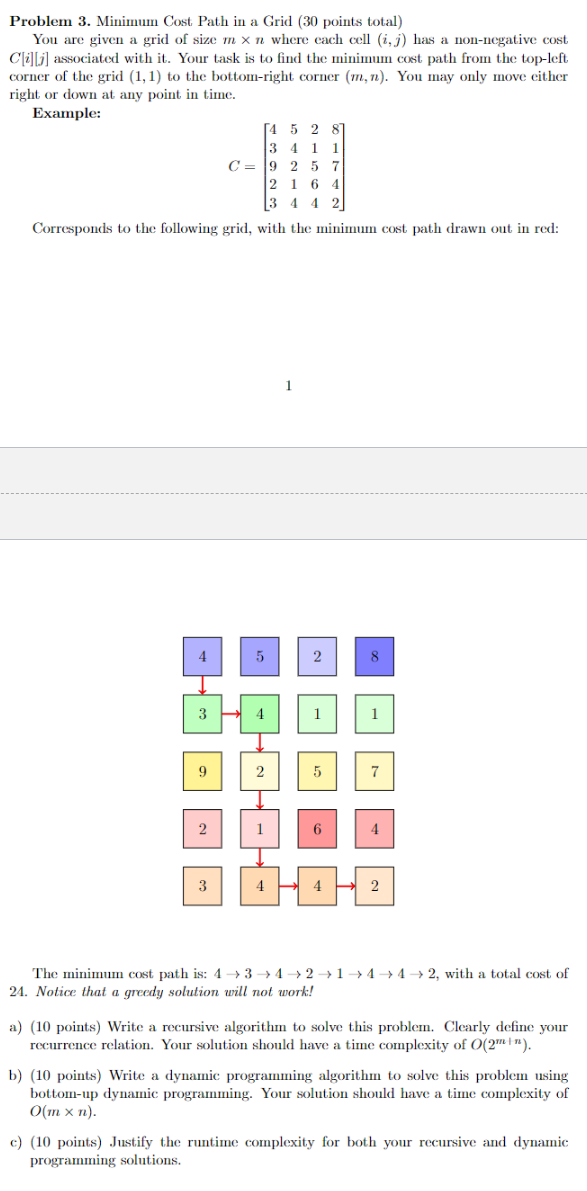
Corresponds to the following grid, with the minimum cost path drawn out in red:

The minimum cost path is: $43421442,$ with a total cost of

Notice that a greedy solution will not work!

a$)(10$ points$)$ Write a recursive algorithm to solve this problem. Clearly define your

recurrence relation. Your solution should have a time complexity of $O(2^{m|n}).$

b$)(10$ points$)$ Write a dynamic programming algorithm to solve this problem using

bottom$-$up dynamic programming. Your solution should have a time complexity of

$O(mn).$

c$)(10$ points$)$ Justify the runtime complexity for both your recursive and dynamic

programming solutions.