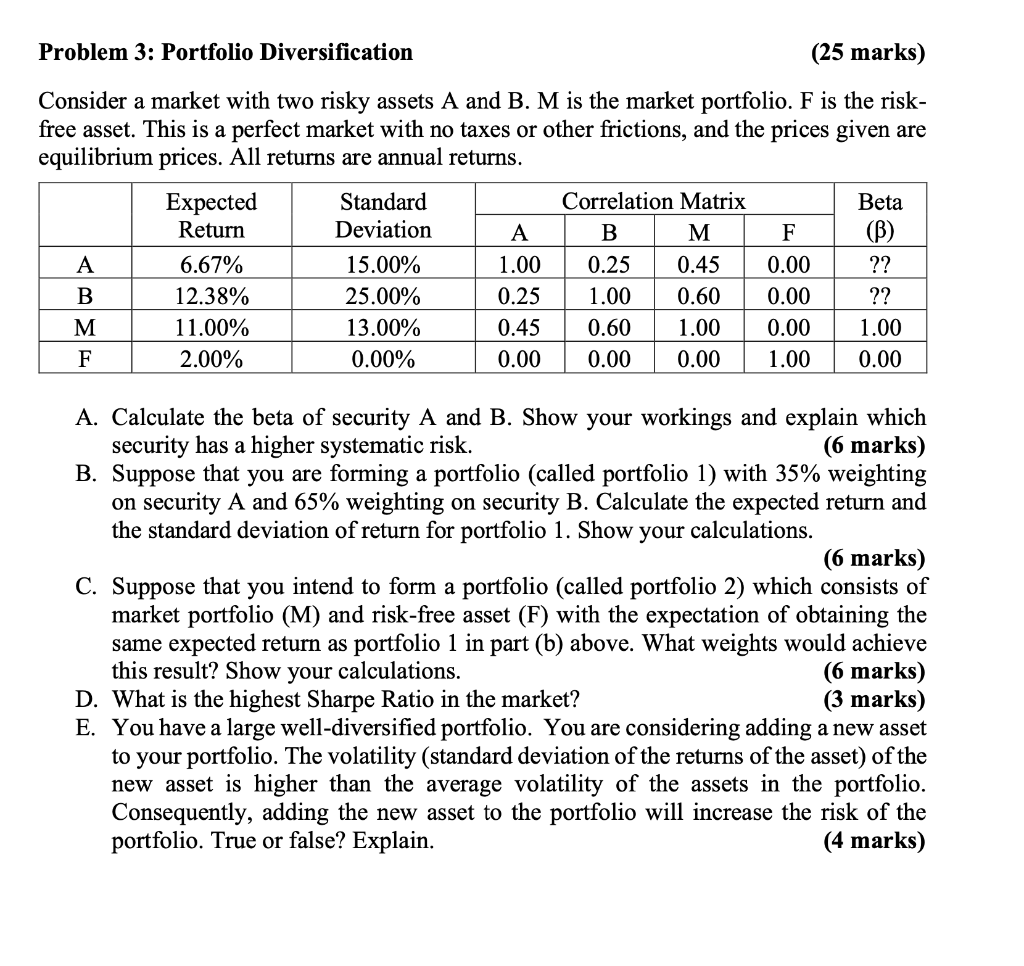
Problem 3: Portfolio Diversification (25 marks) Consider a market with two risky assets A and B. M is the market portfolio. F is the risk- free asset. This is a perfect market with no taxes or other frictions, and the prices given are equilibrium prices. All returns are annual returns. Expected Standard Correlation Matrix Beta Return Deviation A B M F (B) A 6.67% 15.00% 1.00 0.25 0.45 0.00 ?? B 12.38% 25.00% 0.25 1.00 0.60 0.00 ?? M 11.00% 13.00% 0.45 0.60 1.00 0.00 1.00 F 2.00% 0.00% 0.00 0.00 0.00 1.00 0.00 A. Calculate the beta of security A and B. Show your workings and explain which security has a higher systematic risk. (6 marks) B. Suppose that you are forming a portfolio (called portfolio 1) with 35% weighting on security A and 65% weighting on security B. Calculate the expected return and the standard deviation of return for portfolio 1. Show your calculations. (6 marks) C. Suppose that you intend to form a portfolio (called portfolio 2) which consists of market portfolio (M) and risk-free asset (F) with the expectation of obtaining the same expected return as portfolio 1 in part (b) above. What weights would achieve this result? Show your calculations. (6 marks) D. What is the highest Sharpe Ratio in the market? (3 marks) E. You have a large well-diversified portfolio. You are considering adding a new asset to your portfolio. The volatility (standard deviation of the returns of the asset) of the new asset is higher than the average volatility of the assets in the portfolio. Consequently, adding the new asset to the portfolio will increase the risk of the portfolio. True or false? Explain. (4 marks) Problem 3: Portfolio Diversification (25 marks) Consider a market with two risky assets A and B. M is the market portfolio. F is the risk- free asset. This is a perfect market with no taxes or other frictions, and the prices given are equilibrium prices. All returns are annual returns. Expected Standard Correlation Matrix Beta Return Deviation A B M F (B) A 6.67% 15.00% 1.00 0.25 0.45 0.00 ?? B 12.38% 25.00% 0.25 1.00 0.60 0.00 ?? M 11.00% 13.00% 0.45 0.60 1.00 0.00 1.00 F 2.00% 0.00% 0.00 0.00 0.00 1.00 0.00 A. Calculate the beta of security A and B. Show your workings and explain which security has a higher systematic risk. (6 marks) B. Suppose that you are forming a portfolio (called portfolio 1) with 35% weighting on security A and 65% weighting on security B. Calculate the expected return and the standard deviation of return for portfolio 1. Show your calculations. (6 marks) C. Suppose that you intend to form a portfolio (called portfolio 2) which consists of market portfolio (M) and risk-free asset (F) with the expectation of obtaining the same expected return as portfolio 1 in part (b) above. What weights would achieve this result? Show your calculations. (6 marks) D. What is the highest Sharpe Ratio in the market? (3 marks) E. You have a large well-diversified portfolio. You are considering adding a new asset to your portfolio. The volatility (standard deviation of the returns of the asset) of the new asset is higher than the average volatility of the assets in the portfolio. Consequently, adding the new asset to the portfolio will increase the risk of the portfolio. True or false? Explain. (4 marks)