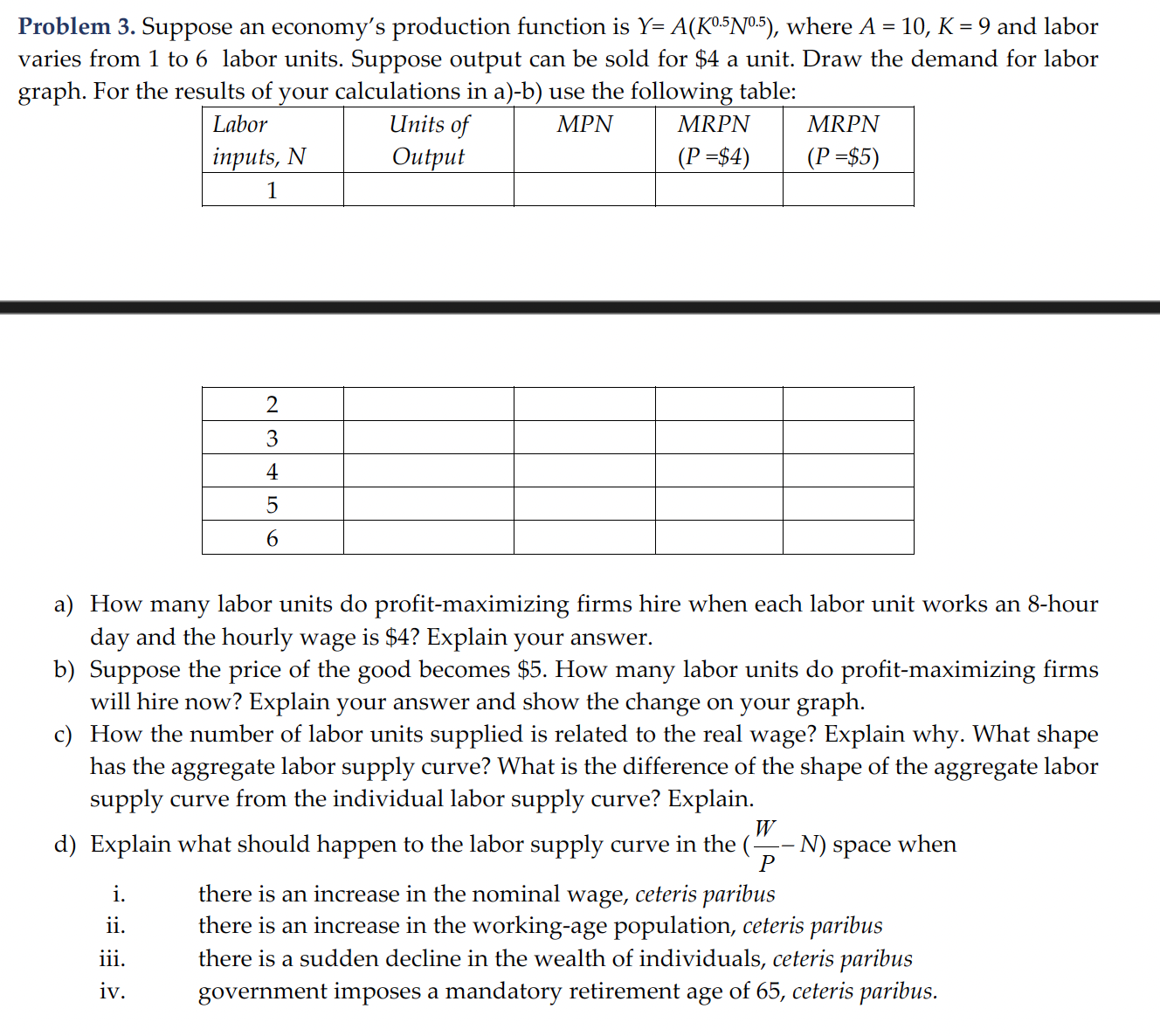
Problem 3. Suppose an economy's production function is Y= A(K0.5 N0.5), where A = 10, K = 9 and labor varies from 1 to 6 labor units. Suppose output can be sold for $4 a unit. Draw the demand for labor graph. For the results of your calculations in a)-b) use the following table: Labor inputs, N 1 2 3 4 5 6 Units of Output MPN MRPN (P=$4) MRPN (P=$5) a) How many labor units do profit-maximizing firms hire when each labor unit works an 8-hour day and the hourly wage is $4? Explain your answer. b) Suppose the price of the good becomes $5. How many labor units do profit-maximizing firms will hire now? Explain your answer and show the change on your graph. c) How the number of labor units supplied is related to the real wage? Explain why. What shape has the aggregate labor supply curve? What is the difference of the shape of the aggregate labor supply curve from the individual labor supply curve? Explain. d) Explain what should happen to the labor supply curve in the i. ii. iii. iv. W P -N) space when there is an increase in the nominal wage, ceteris paribus there is an increase in the working-age population, ceteris paribus there is a sudden decline in the wealth of individuals, ceteris paribus government imposes a mandatory retirement age of 65, ceteris paribus.