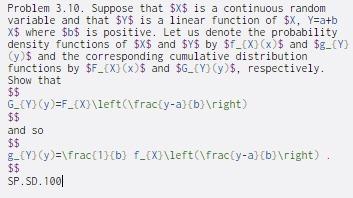
Problem 3.10. Suppose that $X$ is a continuous random variable and that $y$ is a linear function of $X, Y=a+b X$ where $b$ is positive. Let us denote the probability density functions of $X$ and $y$ by $f_(X)(x)$ and $g_(Y) y $ and the corresponding cumulative distribution functions by $F_(X)(x)$ and $G_(Y) (y)$, respectively. Show that $$ G_{Y}(y)=F_{X}\left(\frac{y-a}{b} ight) $$ and so $$ E-(Y) (y)=\frac{1}{b} f_{X}\left(\frac{y-a] [b] ight) $$ SP.SD. 1001