Problem $4$: $(25$ points$)$

Throughout this problem, assume the graphs are undirected and represented by adjacency lists.

a$.$ A graph $\backslash (\backslash$mathrm$\{$G$\}(\backslash$mathrm$\{$V$\},\backslash$mathrm$\{$E$\})\backslash )$ is called bipartite if we can partition V into two non$-$overlapping sets $\backslash ($ V$\_\{1\}\backslash )$ and $\backslash ($ V$\_\{2\}\backslash )$ where $\backslash ($ V$=$V$\_\{1\}\backslash$cup V$\_\{2\}\backslash )$ such that every edge in $\backslash ($ G $\backslash )$ is between a node in $\backslash ($ V$\_\{1\}\backslash )$ and a node in $\backslash ($ V$\_\{2\}\backslash ).$ Using on a graph traversal technique, write an algorithm that takes as input an undirected graph G$,$ and returns whether or not G is bipartite. Derive the time complexity of your algorithm.

b$.$ Same as part $($a$)$ except this time your algorithm has to check if the input graph is a full binary tree. Again, analyze the time complexity of your algorithm.

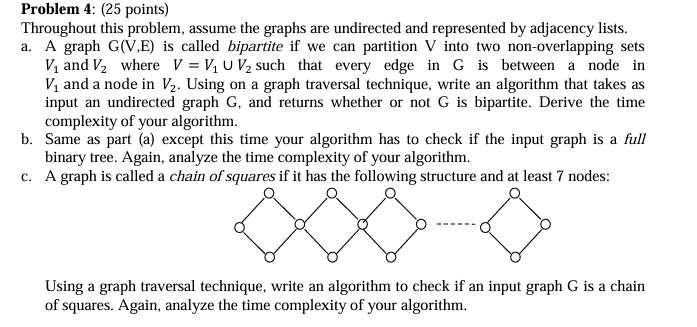
c$.$ A graph is called a chain of squares if it has the following structure and at least $7$ nodes:

Using a graph traversal technique, write an algorithm to check if an input graph G is a chain of squares. Again, analyze the time complexity of your algorithm.