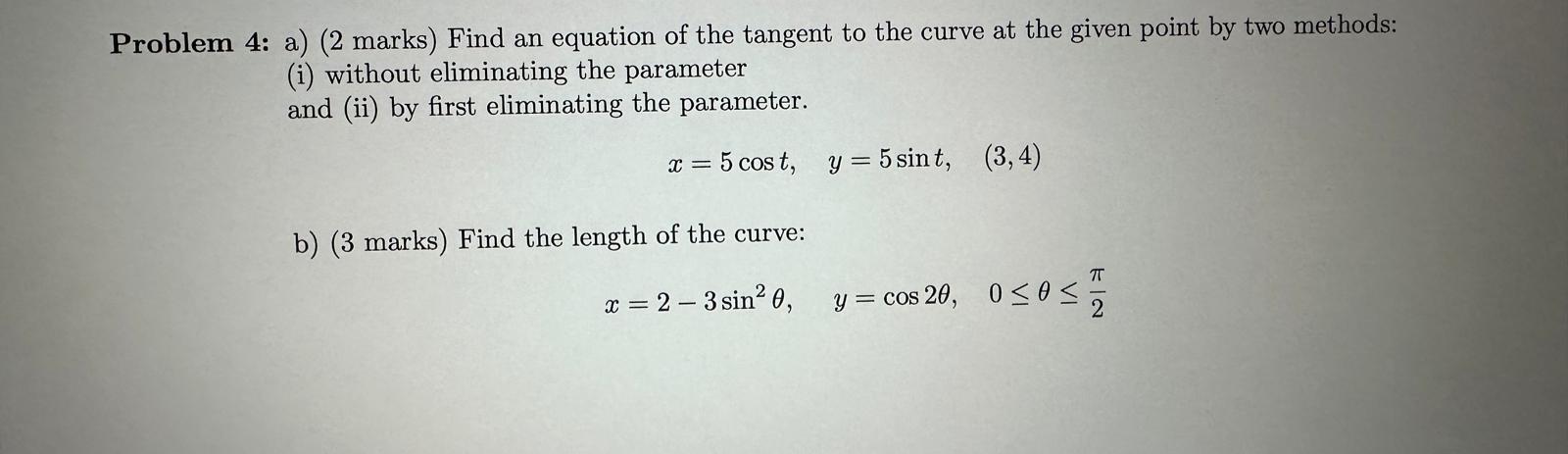
Problem 4: a) (2 marks) Find an equation of the tangent to the curve at the given point by two methods: (i) without eliminating the parameter and (ii) by first eliminating the parameter. x = 5 cost, y = 5 sint, (3,4) b) (3 marks) Find the length of the curve: x = 2-3 sin 0, y= cos 20, 00 2 Problem 3: Let f (x)=1+x+x + x + x + x5. 1. (1 mark) Find T3(x), the Taylor polynomial of f at x = O with degree 3 by using the definition of Taylor polynomials. Note that no partial mark will be given if the answer does not show work of using the definition of Taylor polynomials. 2. (1 mark) Find the remainder R3(x) = f(x) - T3(x). 3. (1 mark) Find the maximum value of f(4) (x) on the interval |x| 0.1. 4. (2 marks) Justify that Taylor's inequality holds true for R3(0.1) using your result from the previous question. theda